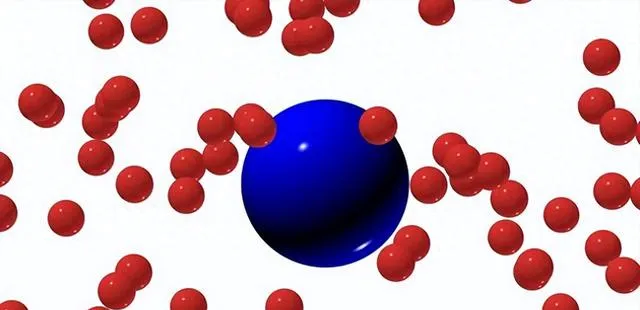
布朗運動是指懸浮在液體或氣體中的微粒所做的永不停息的無規則運動。它最早是由羅拔-布朗在19世紀描述的,當時他觀察到小的花粉顆粒以顫抖的方式移動。這種運動已經成為一個深入研究的課題,並導致了整個科學的眾多進步。
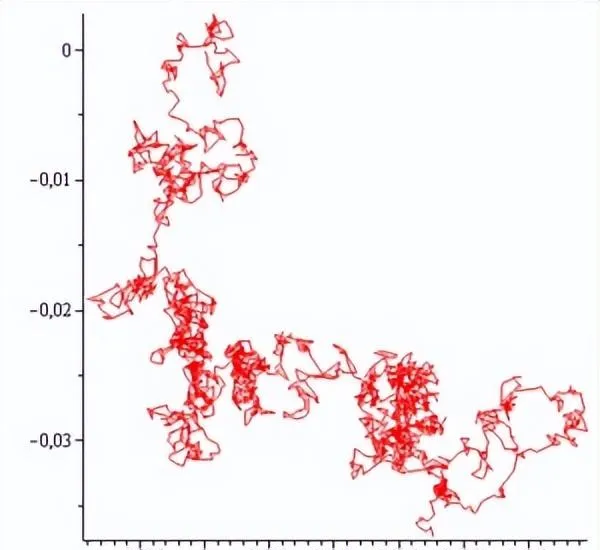
當羅拔-布朗描述這種運動時,氣體的動力學理論正在發展中,該理論將氣體描述為一群隨機地相互碰撞的粒子。當我們觀察到越來越多的這種隨機相互作用時,溫度和壓力之類的量就開始出現了。
進入20世紀後,這種理論仍有爭議,統計力學也沒有被完全接受。然後,愛因斯坦出現了。他在1905年和1908年發表了兩篇論文,將布朗運動正式化,並布置了具體的實驗來證明氣體的動力學理論是真實的。這些實驗是由讓·巴蒂斯特·佩林( Jean Baptiste Perrin)完成的,他驗證了愛因斯坦的理論,並證明了氣體動力學理論的準確性。佩林因為這個實驗在1926年獲得了諾貝爾物理學獎。
這是物理學的一個重大發展,對我們對宇宙的理解產生了巨大影響。到目前為止,我只籠統地談了布朗運動。如果能有一些具體的方程式來談,那就更好了。不幸的是,愛因斯坦的描述並不容易理解。我們將使用保羅-朗格文的理論,他聲稱他的推理是 "無限簡單的"。

朗溫做了很多工作。他的貢獻包括提出 "孿生佯謬",利用超聲波定位潛艇的專利,以及在順磁性和抗磁性方面的大量工作。他還因與瑪麗-居禮有染而受到議論(她是寡婦,但他是已婚)。在這篇文章中,我們將看一下他對布朗運動的正式描述的推導。
郎之萬從以下方程式出發,這是統計力學的一個結果。
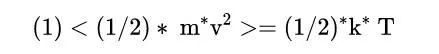
其中m是質素,v是速度,k是波茲曼常數,T是溫度。請註意,符號"<>"表示我們在取平均量。這個方程式適用於一定體積的氣體,所以左手邊是該氣體中每個粒子的平均值。
現在,讓我們挑出一個質素為m的特定粒子。我們發現有兩個力作用於它。第一個是阻力,我們用-F*v來表示,其中F是一個常數,取決於粒子(我們假設F對每個粒子都是一樣的),v是速度。第二個是由B給出的,它代表粒子的隨機 "波動"。我們假設B的平均值是0。
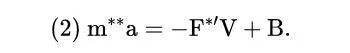
如果你把每項都乘以x,然後用乘積法則做一些變換,你會得到下面的方程式式。

試著自己推導一下吧。
現在,取每個項的<>。也就是說,對我們體積中的每個粒子進行平均。得到了:
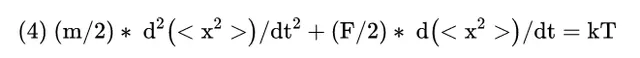
我做了一點整理,但也註意到B*x項沒有了。為什麽我們可以消掉它?之前我說過,我們假設B的平均值是0。這意味著當我們觀察體積中每個粒子所經歷的隨機碰撞時,它會被抵消掉。因為我們假設一個粒子所經歷的隨機波動(B)與它的位置(x)沒有關系,這是一個很大的假設,其他人已經在沒有這個假設的情況下完成了這個推導。
這個方程式是可解的。我們來求<x>的一次導數的解。我得到
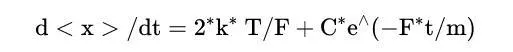
其中C是任意常數。朗之萬指出指數項是無關緊要的。去掉這一項並求解<x>得到解:
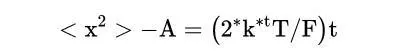
其中<x^2>的初始值為A。這是一個非常強大的方程式!它使我們能夠估計 "擴散 "的程度。它允許我們純粹透過了解氣體的溫度(T)和粒子的微觀內容(F),來估計氣體是如何「擴散」的。布朗運動是一個令人難以置信的工具,它使我們能夠將微觀運動與宏觀動力學聯系起來!推匯出這個方程式是至關重要的。推匯出這個方程式是理解隨機過程的關鍵步驟。
這個解也非常類似於我在這篇文章中描述的 "隨機波動 "情況,但它反而被套用於理想化的氣體。
如果你有興趣閱讀更多關於布朗運動的文章,我強烈推薦這本書。我是從這本書中得到這個推導的。你會發現,即使在第一章,這些想法也可以進一步得到非常有趣的結果。












