內容提要
本文講述了如何利用歐幾裏得用平面幾何方法證明的命題解一元二次方程式,解法別開生面,獨具一格。
接下來拓展介紹了南宋數學家楊輝解一元二次方程式的古法:四因積步法。
最後總結了古法的步驟,負根的意義並點評了古人的局限。
從【幾何原本】的命題談起
集大成也者,金聲而玉振之也。
——【孟子·萬章下】
歐幾裏得可謂古希臘數學之集大成者。在他編寫的【幾何原本】第二卷中有下面兩個命題:
命題05 若一直線既被截成相等的線段又被截成不相等的線段,則不相等線段所圍成的矩形與兩截點之間直線上的正方形之和等於一半直線上的正方形。
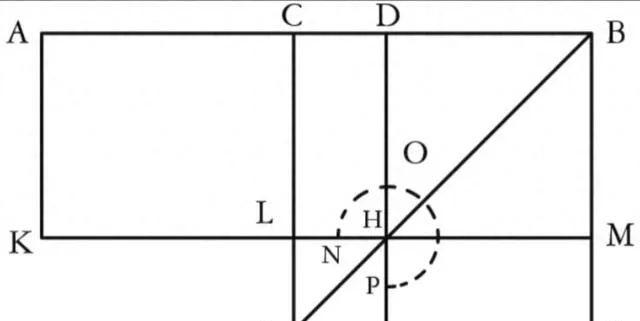
設直線AB在點C被截成相等的線段,在點D被截成不相等的線段。
我說,AD、DB所圍成的矩形與CD上的正方形之和等於CB上的正方形。
命題06 若將一條直線二等分且沿同一直線給它加一條直線,則整條直線與加上的直線所圍成的矩形以及原直線一半上的正方形之和等於原直線一半與加上的直線合成的直線上的正方形。
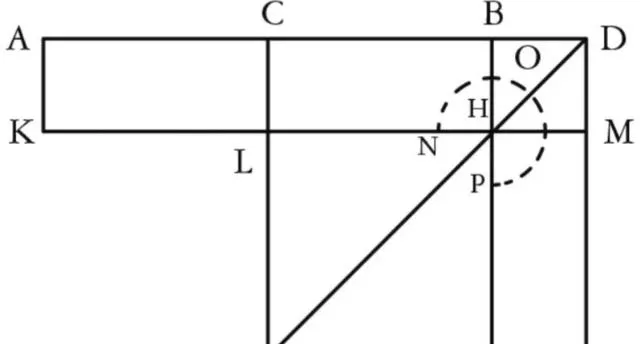
設直線AB被二等分於點C, 且沿同一直線給它加上直線BD; 我說,AD、DB所圍成的矩形與CB上的正方形之和等於CD上的正方形。
這兩個命題是用文字語言敘述的,改為數學語言敘述就清晰易懂了。
命題5相當於下面的恒等式。
圖片
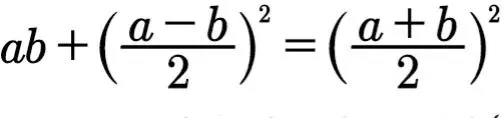
命題6相當於下面的恒等式。
圖片
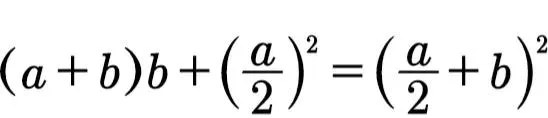
對於x(b-x)=c這種類別的一元二次方程式,可以用命題5來解方程式。
對於x(b+x)=c這種類別的一元二次方程式,可以用命題6來解方程式。
已知一條線段AB長度是b,中點是C,求動點D的位置:(1)點D線上段AB之內,且與中點C不重合,AD·BD=c;
(2)點D線上段AB的延長線上AD·BD=c.
接下來用例題來說明上述解法。
例一 設線段AB的長度為12,點D是AB上的一點。設AD為x,則DB為12-x,AD·DB=32,求AD的長度。
解 據題意可列方程式
x(12-x)=32
可用命題5解這個方程式。
令a=12-x,b=x,則a-b=12-2x,a+b=12,已知ab=32,代入命題5的恒等式,得
圖片
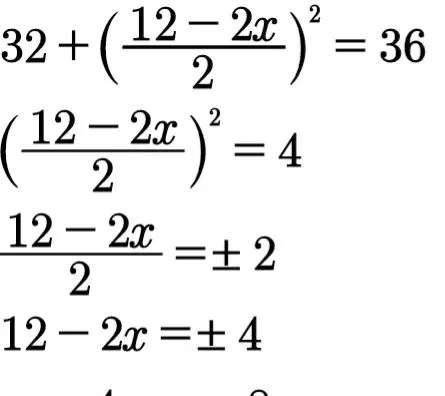
解得兩根為4和8。
例題2 線段AB的長度為12,點D是AB延長線上的一點。設BD為x,則AD為12+x,AD·BD=64,求BD的長度。
解 據題意可列方程式
x(12+x)=64
可用命題6解這個方程式。
將a=12,b=x,(a+b)b=x(12+x)=64代入命題6的恒等式,得
(6+x)²=64+36
6+x=±10
x₁=4,x₂=-16
2019年武漢市元調數學考題第9題
9.古希臘數學家歐幾裏得的【幾何原本】記載,形如x²+ ax =b²的方程式的圖解法是:如圖,畫Rt△ABC , ∠ACB =90°, BC =a/2, AC = b ,再在斜邊 AB 上截取 BD =a/2,則該方程式的一個正根是( )
a . AC的長
b . BC的長
c. AD的長
D . CD的長
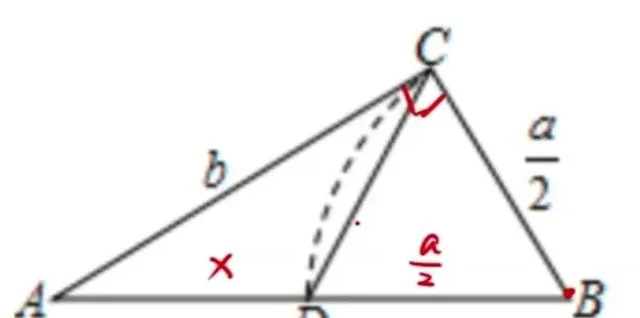
答案是選c。令BC=6,AC=8,則AB=10,方程式x²+12x=8²的一個根是10-6=4
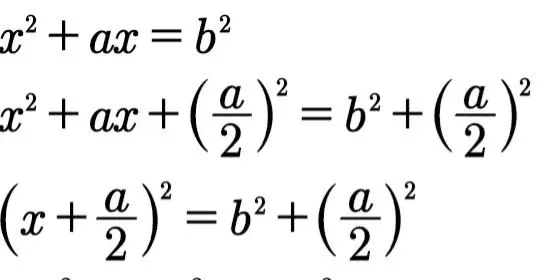
楊輝解方程式
1275年,中國南宋數學家楊輝在【田畝比類乘除捷法】中提出一個問題:「直田積八百六十四步,只雲闊不及長一十二步,問闊及長各幾步?
楊輝解法 解
圖片
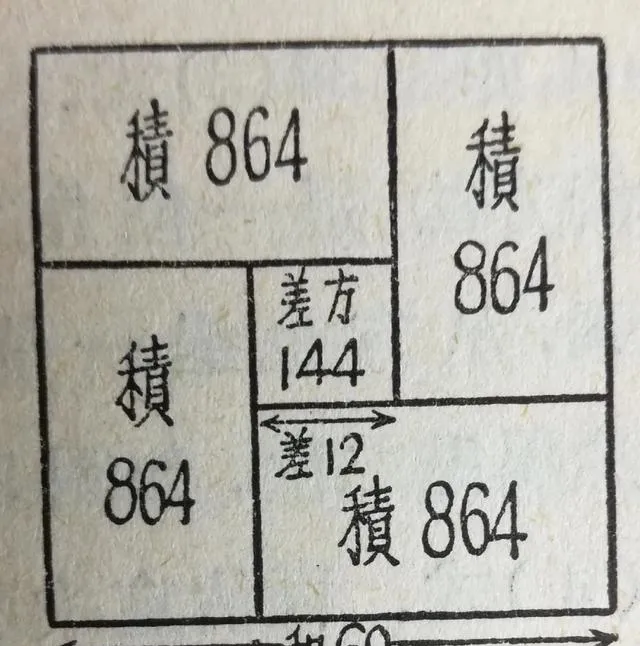
由上圖得恒等式
(a+b)²=(a-b)²+4ab
把ab=864,a-b=12代入恒等式,得
(a+b)²=144+3456
=3600
所以a+b=60
解二元一次方程式組(小學和差問題)
{a+b=60;
a-b=12.}
解得a=36,b=24.
答:直田長36步,寬24步。
本題數碼設計很巧,提供了一個表演速算的素材。
問一天等於多少秒?
答:24×60×60=3600×24=36×24×100,而
36×24=(30+6)(30-6)=30²-6²=900-36=864
所以一天等於86400秒。
中國古代數學家還用這樣的方法解二次方程式:
{x₁+x₂=a;
x₁x₂=b.}
x₁和x₂是方程式的兩個根,是未知數,a和b是已知數。
設x₁為a,x₂為b,x₁>x₂,利用恒等式(a+b)²=(a-b)²+4ab解上面的二元一次方程式組,得
a²=(x₁-x₂)²+4b
(x₁-x₂)²=a²-4b
解得
圖片
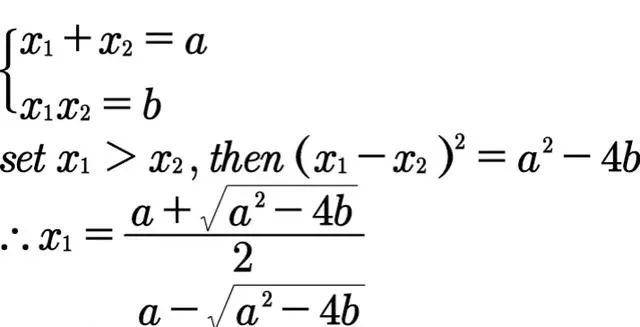
實際上就推匯出了求根公式。
總結和點評
代數的發展可以分為三個階段,即文字敘述的代數和簡字代數及符號代數。【數學辭海】某一卷附錄收錄了1400多個數學符號。而歐幾裏得大約出生於公元前325年,在那個年代代數不發達,沒有適當的代數符號。古希臘人用線段的長度表示數,用文字敘述運算過程,擅長用巧妙的幾何法證明代數恒等式。
【幾何原本】第二卷命題4就是用幾何法證明代數恒等式:(a+b)²=a²+2ab+b²
命題04 若任截一直線,則整條直線上的正方形等於各線段上的正方形與兩線段所圍成矩形的二倍之和。
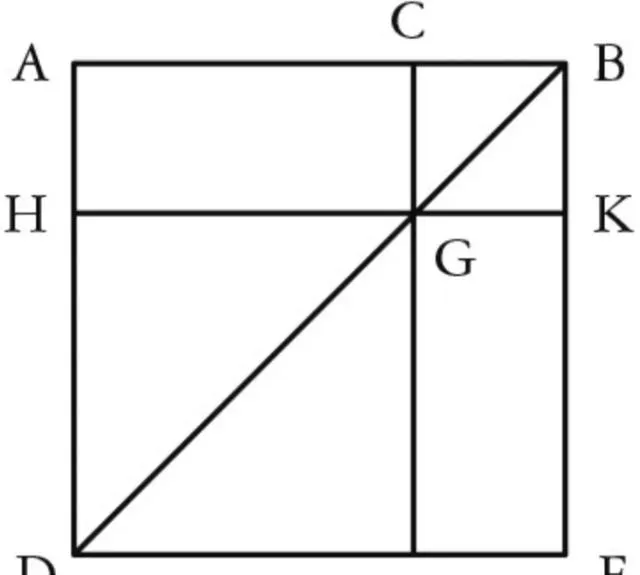
設直線AB被任截於點C; 我說,AB上的正方形等於AC、CB上的正方形與AC、CB所圍成矩形的二倍之和。
命題5證明了另外一個重要的恒等式(a+b)²=(a-b)²+4ab的變式。
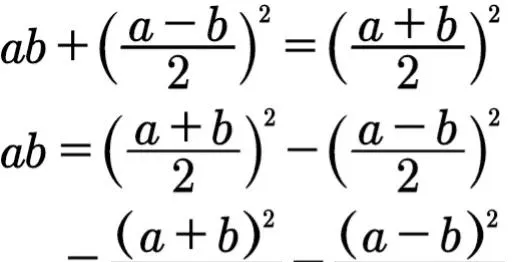
還有一個變式:
用命題4解一元二次方程式大家都熟悉,就從略。用命題5解一元二次方程式的步驟如下:
先把方程式覆寫成x(b±x)=c的形式。設x為a,b±x為b,根據題目條件求出a和b的和、差、積。再把上述和差積代入恒等式,可以知二求一。把方程式降次為兩個一次方程式就解得a和b了。
例題三 解方程式x²+10x=39.
解 原式可以覆寫成:x(10+x)=39
則a+b=10+2x,a-b=10,ab=39,代入恒等式得
(2x+10)²=10²+4×39=256
兩邊同時開平方,
2x+10=±16
∴x₁=3,x₂=-13
阿拉伯數學家和歐洲數學家在歷史上曾經不承認和排斥負數,所以常認為方程式的負根無意義而舍棄。那麽,問題來了,這個方程式的負根有沒有意義?
根據歐幾裏得的命題,負根有意義。
線段AB在正方向的延長線上有一點D,已知AB=10,設BD=x,則AD=10+x。又知道BD和AD圍成了面積為39的長方形,求BD的長度。
方程式的兩根告訴我們,從點B出發,沿正方向延長3就找到符合題意的點D,或沿反方向前進13,也可以得到符合題意的點D。有向線段的長度,正方向為正,反方向為負。這就是負根的意義。線段AB的中點是C,站在中點C的角度看,方程式的兩根是關於中點對稱的。總之,方程式的負根是有意義的。
此外,代數基本定理告訴我們,二次方程式的根不少於兩個,也不多余兩個,恰好有兩個根。好比一枚硬幣有兩面。特例是判別式等於零,方程式有兩個相同的重根。好比硬幣的兩面都是一樣的。
圖片
古人受到時代的局限,對此認識不足。
科學尚未普及,媒體還需努力。感謝閱讀,再見。











