「中國孩子數學能力獨步全球」,你是不是也曾將這樣的神話誤認為事實?
最近,一條關於留學教育的影片幾乎火遍了各個平台,談論的核心問題就是「數學」,只不過以影片中被采訪者的經歷來看,事實恰恰相反: 中國留學生的數學水平真心比不過美國大學生 。

「論計算,中國學生一等一」,但美國學生的學習更強調分析、推測等數學的底層邏輯,而這恰恰是中國學生所缺乏的,以至於去了美國之後往往反映數學吃不消……
同樣提及國內數學教育與國際的差距,幾年前,中國科學院物理所研究員曹則賢教授在中國科學技術大學的演講中所列出的數據則更加驚人,他說, 85%的數學知識從來沒有傳入到中國 。
這也能從一定程度上解釋,為什麽大家的「數學焦慮」會如此普遍而深重:微博上與數學有關的話題達到了5.9億人次的閱讀;而抖音裏,數學的話題播放量高達541億次,平均每個中國人都要觀看至少38條關於數學的影片。
數學為什麽難學?為什麽讓絕大多數接觸到它的人感到恐懼?
今天,阿信要向所有被數學折磨,以及對數學感興趣的小夥伴強烈推薦一本能補齊數學知識拼圖的新書——
【數學的邏輯】
。

作者是劍橋大學數學博士、芝加哥藝術學院常駐科學家
鄭樂雋
。
「消除世界上所有人對數學的恐懼」是鄭教授終身奮鬥的事業目標。為此,她寫作了【超越無窮大】【數學思維】【邏輯的力量】等多部數學科普暢銷書,被英國【衛報】曾授予「科學與自然類新秀作者」獎。
同時,她還是一位舉辦過音樂會的鋼琴家,能夠流利用法語、英語和廣東話交流。
在這本書中,她講告訴你,數學的核心,從來不在於計算出正確結果,數學是一整套思想的整合,邏輯在其中起著至關重要的作用。
掌握了數學的邏輯,你會發現,數學並不枯燥,相反,它與我們生活中的方方面面都息息相關,用數學思維觀察世界,你會獲得一種全然不同的視角。
鄭樂雋:從厭學少年到數學達人
和很多普通人一樣,
鄭樂雋
對數學也是有厭學情緒的:
我和它的感情在小學階段不斷惡化,到了初中我開始徹底厭惡這門學科,因為我覺得它既乏味又迂腐。
我一點兒也不責怪我的老師,這都是課程設定和考試制度的問題。

鄭樂雋
但她也和很多人一開始一樣,忽視了一個重要的資訊:人們討厭數學往往是因為找不到正確的答案而覺得自己很愚蠢,並不是討厭尋找的過程。
所幸,她找到了自身原因。
在她開始接觸少許高等數學之後,情況有了一些改觀,尤其是普通中等教育證書(GCSE)的研究專案令她對數學鐘愛有加。
那都是一些開放性的課題,每個學期需要花費幾周的時間來完成。我們從一個結構嚴謹的問題出發,獨立探索由它引發的無限可能性。
直到上了大學,事情才真正開始好轉。等到鄭樂雋開始攻讀博士學位時,她對數學的喜愛程度已經超過了圖表所能表示的範圍。當然,那個時候她們已經不再上課,而是透過閱讀、集體討論、參加研討會來學習。
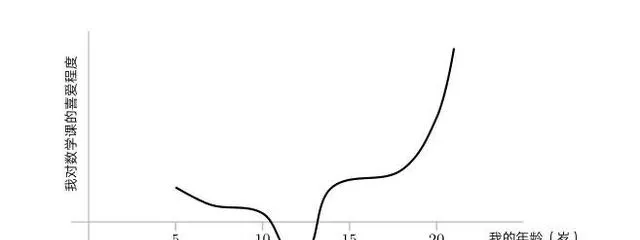
鄭樂雋對數學的喜愛程度變化。圖:【數學的邏輯】
在她之後的人生裏,數學成了
她的愛好,而不是苦難,她將這些經歷寫成了【數學的邏輯】
。

【數學的邏輯】都在說啥?
在【數學的邏輯】的開篇,鄭樂雋就幫助大家撇清自己的「愚笨」。
我想要告訴你,如果你覺得自己不擅長數學,或者在學校裏被認為數學成績很糟糕,那麽完全有可能你只是在探尋對數學更深層次的理解,而身邊沒有人能幫助你達到那個水平。
在前面4章,她都是從廣義的數學概念講起,然後聚焦數學中的一些具體的問題,以故事的形式給大家科普:數學從哪裏來、數學的邏輯、為什麽要學習數學、什麽是好的數學……
在5、6、7三章,她會聚焦具體的數學工具,給大家介紹字母、公式和圖形。
第8章,她用一個貌似天真、有時也被視為「愚蠢」的問題開始講故事,然後透過對這個問題的深入探究把我們引向一項重要的數學研究。
接下來,我們來看看這本書具體講了什麽。
比如在【圖形】這一章,講到很多女孩子對於編發辮感興趣,尤其是對如何編出發辮的不同圖案感興趣。下圖左右分別是法式辮子和瑞典式辮子。

很多人以為這只是一個生活技巧,卻不知道,編發和數學中 高維度範疇論 研究有很大的關系,這項理論研究的出發點就是基於我們不僅關心某物是否發生了互換,而且關心互換的具體方式。
尤其是放到抽象數學領域,我們會研究一般意義上的交換律。尤其是空間交換所帶來的結果是一樣的,比如下面兩張圖。
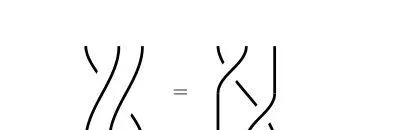
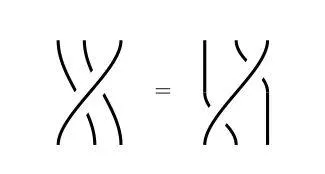
雖然空間發生了位移,但是實際上的編發效果是一樣的。從結果來說,這就是我們在數學中認定辮子結構「相等」的含義,即它們之間的差別僅僅在於移動和拉緊,而與解開和重新纏繞無關。
對數學來說,重要的是證明圖形推理具有邏輯上的正確性。這也是範疇論中關於證明邏輯與直覺相互對應的重要性。

生活中處處都充斥著數學
生活中很多很簡單的案例背後常常有高深的數學的理論,只是我們並不知道「這屬於數學」。
舉一個看起來天真實際能引發深刻意義的數學問題。一個圓有幾條邊?
大多說人會覺得,圓就是一條封閉的曲線,是一條邊。
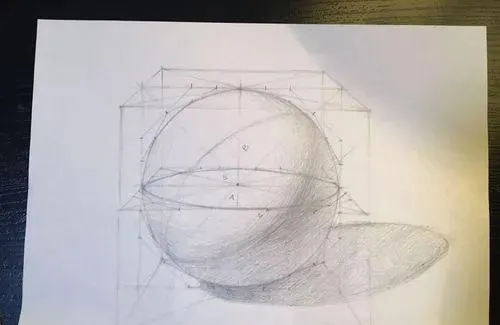
但是學會微積分的人知道,圓是透過無數次切割得來的接近「圓」這個概念的,學素描的人畫圓的時候,最規矩以及最保險的模式也是透過正方形進行無數次的切割得到想到的結果。
所以圓上其實是存在無數條切割的「小邊」的,這個邊,可以是無窮個。
再舉例一個我們生活中的案例。
你覺得一根吸管有幾個洞?
和往常一樣,我們對這個問題產生數學上的興趣並不在於答案究竟是什麽,因為從不同的角度出發能得到不同的正確答案。
真正有趣的是,我們可以用不同的方式來思考洞以及吸管的問題。於是我們回到了計數的方法上:首先,什麽才是可被統計在內的物件;其次,什麽時候兩個物件實際上是相同的。

常規認為,立體角度上吸管只有一個洞,計數為1。但是從平面上看,左右兩邊都是洞,計數為2。重新回到立體角度上,如果吸管內部空間和外部相連,那吸管實際是一個洞都沒有,計數為0。
而從分子角度考慮問題,吸管放大到無窮大,分子之間是有很多空隙的,所以吸管有無數個洞,計數為∞。
因此,
沿襲以往的數學思想,關鍵不在於判斷哪個答案是正確的,而是要確定它們在何種意義上是正確的
。
如果覺得一根吸管只有一個洞,我們該怎樣定義洞?同樣,如果覺得一根吸管有兩個洞,我們就必須采納另一種洞的定義。那我們該怎麽做呢?
拓撲學是專門研究形狀的數學分支,它依據一種特定的「相同」理論判斷哪些形狀與另一些形狀相同。它來自將一個東西逐漸變形為另一個東西的過程。

比如探究吸管只有1個洞的時候,從拓撲學上,我們可以借用甜甜圈的例子。看起來兩個實物沒有什麽關聯,但是如果我們用手指壓扁它的內側壁,最終,甜甜圈會變成一個圓筒,然後我們將其拉長,就變成了一個吸管。
從這個意義上看,吸管的確只有一個洞,我們也可以想象吸管變得越來越短,直到變成一個圓圈,它的中間只有一個洞。
這只是拓撲學研究洞的方法之一。數學家一般不使用「洞」這個名稱,因為我們發現它相當模糊。而且在某些情況下,我們的直覺並不喜歡拓撲學做出的解釋。
所以這本【數學的邏輯】會從根本上讓你知道數學不僅僅是工具,也不僅僅是枯燥的公式,更不是為了驗證你是否聰明的道具。
喜歡數學的人也僅僅是「喜歡數碼」「喜歡公式」或樂於找到正確的答案不同。
鄭樂雋更想告訴大家的是:
人們厭惡數學的原因是非常不幸的,並不是基於數學真正的本質
。
那些天真、開放、「愚蠢」的數學問題絕對是有意義的,它們都是好問題,這樣的問題在數學研究過程中是不可或缺的。
數學,更多的是幫助我們找到找到事物之間關系,也因此能幫助我們發現世界的真相。
*商務合作、高管學習請添加:墨墨老師138 1108 2512 (微信同步)











