為什麽我們在現實生活中會需要三重積分。我們要把它分解開來。我們先來分析一下,為什麽我們需要積分,然後是二重積分,最後是三重積分。
如何理解積分
對於簡單的圖形,我們有現成的公式來求它們的面積。
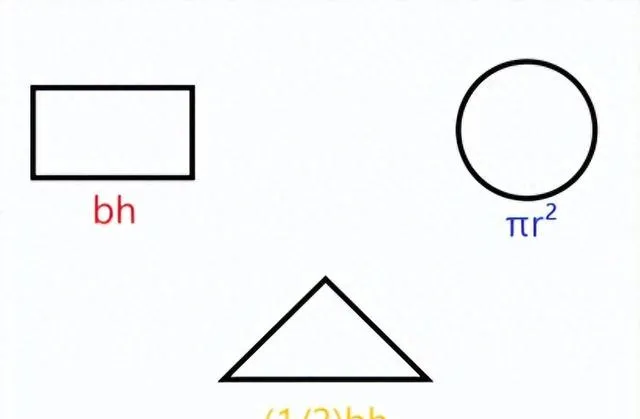
但我們如何求下面圖形的面積呢?

答案是,我們可以使用積分。描這裏的積分就可以理解為曲線下面的面積。假設我們想求一條奇怪的曲線下面的面積,它看起來像這樣:
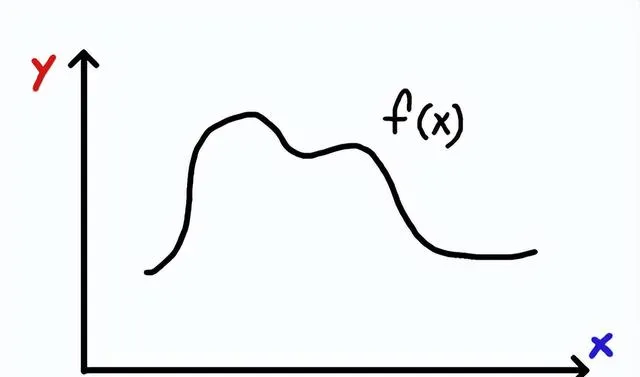
用公式法求這樣的面積是很困難的。我們希望用更簡單的形狀去近似或者代替它,比如矩形,面積公式是長乘以寬。那我們為什麽不在曲線下畫一堆矩形,求這些矩形的面積,然後把所有的小矩形面積加起來,來近似計算曲線下的面積,就像這樣:
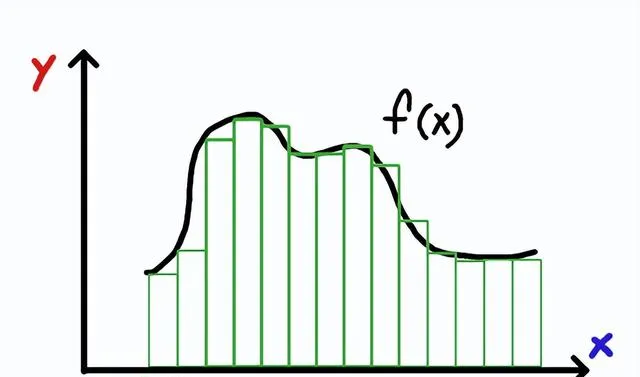
這是個不錯的近似值,值為所有綠色矩形的面積之和。
每個矩形都有相同的寬度,以使計算更容易。寬度等於一個我們稱之為Δx的量(概念上,Δx是x的變化)。每個矩形的高度是不同的,但它是由函數f(x)給出的,由圖中彎曲的黑線表示。
為了體現高度是不同的,從左邊開始的第一個矩形的高度是f(x),第二個矩形的高度是f(x),以此類推。一般來說,第i個矩形的高度為f(x)。
矩形的面積是高度乘以寬度,所以其中一個矩形的面積等於f(x)*Δx。如果我們把所有的矩形面積加起來,我們就可以得到曲線下的近似面積。
但是我們的近似值並不那麽精確,我們可以透過增加矩形的數量使近似值更準確,就像這樣:
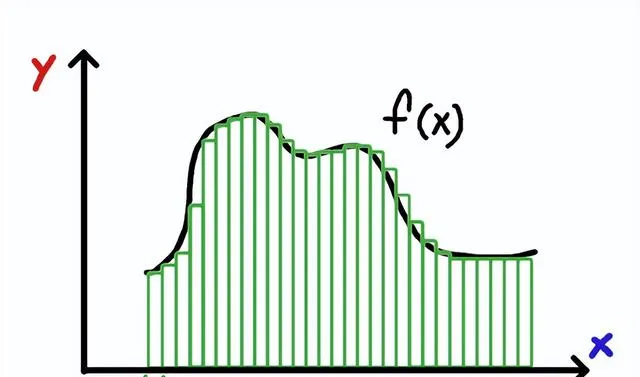
註意,Δx現在更小了。而且,這個和比上一個更準確。我們可以繼續把圖形分成越來越小的矩形,使值更加精確。最終,隨著矩形的數量接近無窮大(每個矩形的寬度接近0),近似面積越來越接近實際面積。
這個總和被稱為積分。積分就是這樣寫出來的。

積分符號∫看起來像一個大的S。當一個叫哥特佛萊德-萊布尼茨的德國人發展微積分時,他認為積分是一個無限的和。dx "代表Δx,即每個矩形的寬度,它現在是無限小的。這個 "dx "被稱為微分。
這就是我們如何使用(一重)積分的方法。 我們對1個變量進行積分,在這個例子中是x。 當沿著x軸移動時,我們取一堆無限小的長方形的總和。寬度越小,近似值就越精確。
如何理解雙重積分
對於二維圖形我們求的是面積,對於三維圖形我們求的是體積。像以前一樣,我們對一些三維圖形的體積有漂亮、整齊的公式。
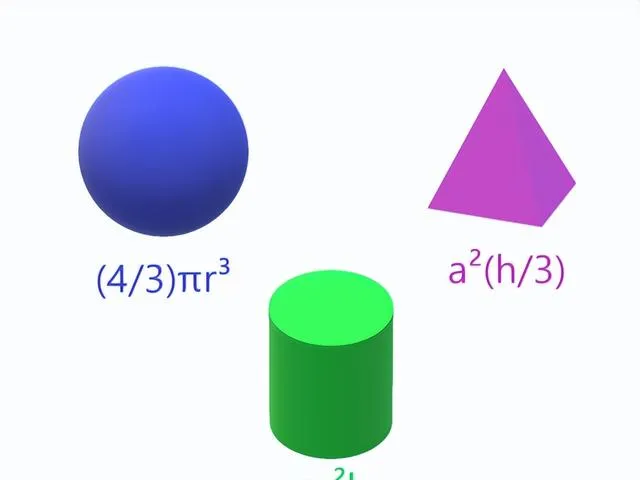
但要求這些三維圖形的體積就難多了。

我們應該如何求出這些奇怪形狀的體積呢?為了求出體積,我們將使用雙重積分工具。比方說,我想求出這個麪包的體積。
我們可以從近似的體積開始。我們可以先把這個大塊的麪包沿著Y軸分成很多片。

每一片都有相同的寬度,我們把這個寬度稱為Δy。如果我們把所有片的體積加起來,就可以得到這個麪包的大致體積。當我們把麪包分成越來越薄的片時(Δy越來越接近於0),麪包體積的近似值會越來越精確。
所以我們只需將所有麪包片的體積相加即可。唯一的問題是,計算一個麪包片的體積並不那麽容易。如果我們看一下單個的麪包片,你會發現它本身還是一種奇怪的形狀。

我們需要對這塊麪包片的面積進行近似計算,我們可以透過把它分成一堆矩形來實作。換句話說,為了求出一片麪包的面積,我們必須像上面那樣進行一重積分。

我們在X軸上進行積分,把小矩形加起來。然後,回到麪包上,我們在Y軸上積分,把所有麪包片的體積加起來。
從本質上講,要求出麪包的體積,我們要求積分的積分:我們求麪包片的和,每個麪包片本身是矩形的和。當然,"積分的積分 "寫起來很麻煩,所以我們就叫它雙重積分,我們這樣寫:

這就是二重積分(雙重積分)。這是什麽意思?
「dy 」是麪包片的寬度,"dx "是麪包片中矩形的寬度。f(x,y)指的是麪包的「頂部」。這是因為麪包在某一點的高度(又稱z座標)是該點的x座標和y座標的函數,所以它是f(x,y)。
如何理解三重積分
到了本文的重點:三重積分。我們已經講過了一重積分和二重積分。希望大家能明白為什麽這些東西會有用處:雖然這不是它們的唯一用途,但它們可以幫助我們求出不規則的二維和三維圖形的面積和體積
你可能會猜到,這裏有一個規律,是這樣的:
你是對的! 三重積分是用來求一個四維形狀的體積的。這聽起來不可能。你可能會說:"我們並不生活在四維空間,四維形狀不存在"。我可以解釋三重積分在現實世界中是如何使用的。要明白這一點,我們需要改變我們對維度的思考方式。
一張照片裏有多少個維度?
讓我們回到二重積分的話題上來。你見過熱成像嗎是用熱像儀拍攝的照片,不同的顏色代表不同的溫度。
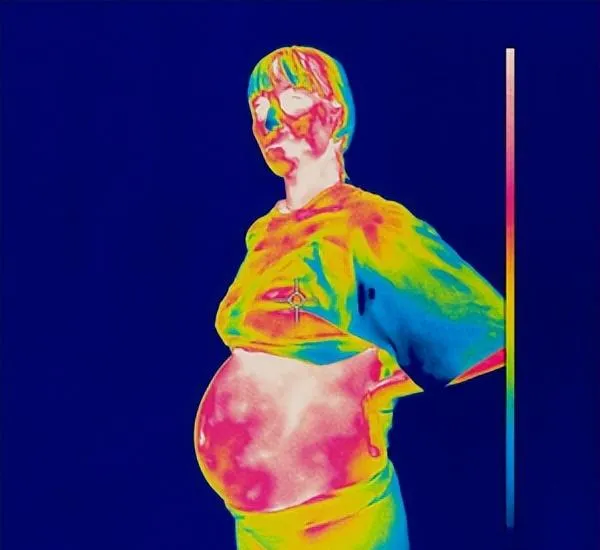
照片是二維的,但熱成像照片上的每個點都有一個與之相關的 "熱量"。由於熱量是用數值表示的,我們可說,熱成像照片上的每一個點都有一個與之相關的數碼。

從右邊的圖例可以看出,藍色斑點的熱值可能是 "15",而較紅的斑點的熱值可能是 "28"。我們甚至可以把這張照片變成三維圖,其中高度(z座標)與熱量相對應。
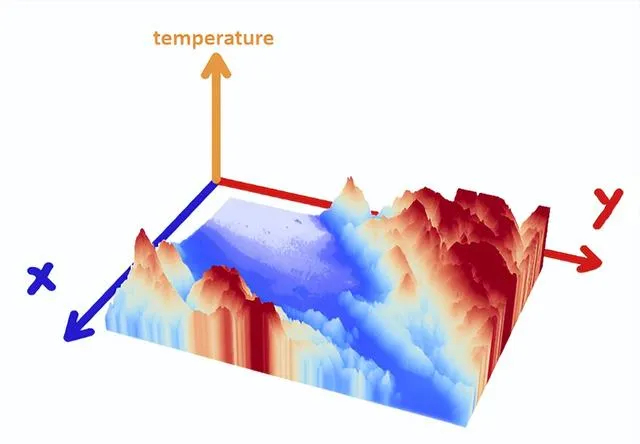
那麽,這裏有一個問題:我如何求出這整張照片的總熱量?答案是我們用二重積分。我們在x軸和y軸上積分,然後把整個照片的溫度加起來。總熱量等於上面三維圖的體積。
這似乎令人困惑,因為這張照片是二維的,而如前所述,雙積分是用來求三維形狀的體積的。但我們需要改變對 "維度 "的思考方式。 我們通常認為維度是空間維度。然而,一個 "維度 "實際上只是指與一個點相關的數值。一個維度不一定是空間中的一個方向。
現實世界中的三重積分
回到三重積分的話題。比方說,你有一間形狀像盒子的臥室。暖氣口可能只在房間的一個角落,所以熱量並沒有均勻地分布在整個房間。溫度在通風口附近會很高,在與通風口相對的角落會很低,以此類推。房間裏任何一個點的熱量都由某個函數f(x,y,z)給出。
如果我想把房間裏的所有熱量加起來,我該怎麽做?
很明顯,房間裏有三個空間維度。但同樣,溫度也算作一個維度,因為它是一個與點相關的數碼。所以這個問題發生在4個維度上:寬度、長度、高度和溫度。
由於有4個維度,我們將使用三重積分。
讓我們先把房間視覺化。這就是一個三維房間的熱量圖。
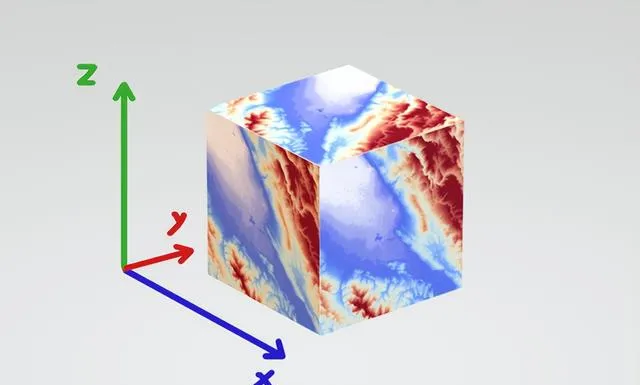
如前所述,如果你看這個房間,溫度是盒子內一個點的x、y和z座標的函數。這個函數是f(x,y,z)。
我們將從Z軸上的積分開始,把盒子分成許多平行於地面的「切片」。
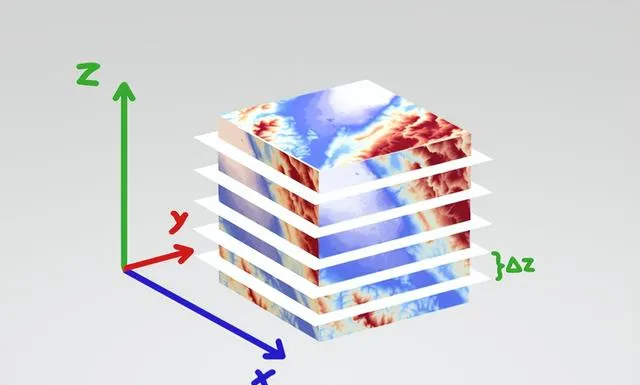
乍看起來,我好像把房間分成了一堆二維的切片,但請記住,溫度也是一個維度。我實際上是把房間切成了一堆二維的溫度圖。而正如我們所討論的,二維溫度圖有三個維度。
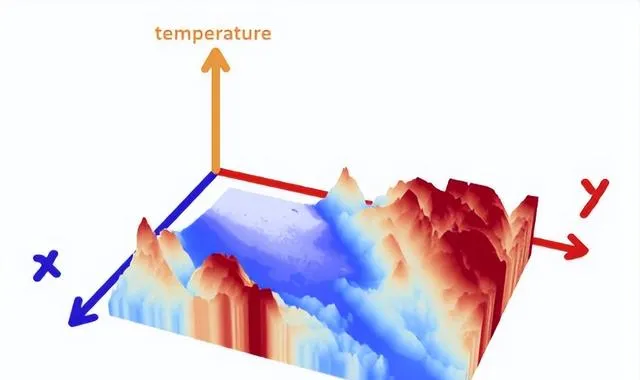
接下來,我們要對y積分,把熱圖分成許多小片,就像我們對麪包做的那樣

:
最後,我們將把每一個切片沿著X軸劃分成許多小矩形。
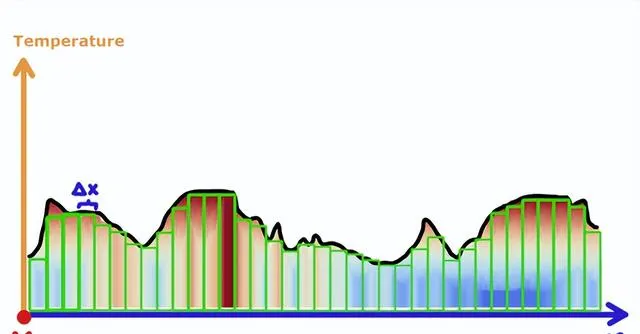
這樣,我們可以準確地把這個房間裏的所有熱量加起來。我們沿Z軸將房間分成熱圖,然後沿Y軸將熱圖分成片狀,再沿X軸將片狀分成矩形。我們把這稱為三重積分。它是這樣寫的:
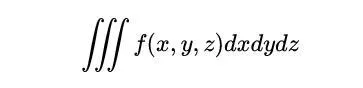
「dz」 是z的變化,"dy "是y的變化,而 "dx "是x的變化。
使用這個三重積分,我們可以求出3維房間裏的總熱量。如果一個 "維度 "可以指空間維度以外的東西,我們就會發現三重積分有很多套用。我們可以求出一些三維物體的總慣性,或者籃球的重力。
結論
簡而言之。就數學而言,一個維度不一定是指空間。它可以指任何數值,如溫度、慣性、或濕度。
所以,我們用三重積分來尋找四維圖形的體積,這乍聽起來沒什麽用。但是,只要我們轉變一下對 "維度 "的思考方式,就會發現四維圖形比看起來更常見。三重積分幫助我們認識和理解這些形狀。











