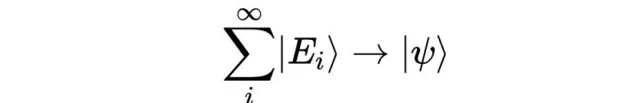如同春風拂面,這正是量子力學為何必須運用「希爾伯特空間」的根本原因。在前文中,我們探討了量子力學中的向量空間並介紹了態向量:粒子的量子狀態可透過向量空間的態向量來表達。任何物理量的量子態能夠被視作該物理量所有可能結果態的線性組合,並且這些結果態的列表可能是無限的。

此時我有一個簡單卻至關重要的問題要問:那個量子態的向量空間,它的維度到底是多少呢?這裏要特別註意,向量空間的維度實際上是構成基的向量的數量。既然如此,那麽在這個向量空間中,基到底包含多少向量呢?量子態或特許以是無數結果態的線性組合。盡管目前還沒有證明這些結果側的列表構成了一個基,但我們可以暫且假定這點(後續的文章中會進一步驗證)。這就意味著,基可能會包含無限多個向量,因此向量空間的維度也可能是無窮大!
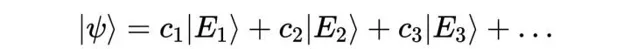
聽起來似乎有點不可思議,然而我們確實需要一個無限維度的概念,來用線性代數表述粒子狀況。理論上,這一切似乎都很合理,然而當「無窮」這一概念被引入時,確實需要謹慎行事。為了闡明線上性代數中引入「無窮」可能導致的問題,接下來讓我們考察一個具體的向量空間範例:實數上多項式構成的向量空間。只有當一組物件滿足某些特定規則時,它們才能算作向量空間,這一點很容易驗證。

多項式自然地組成一個向量空間,我們可以選取x的所有冪次作為基,從零次冪開始。借助這個基,任何多項式都能被表示為這些基元素的線性組合。現在,若我們將這些線性組合擴充套件到無窮,會發生什麽呢?我們利用基構建一個帶有精心選定系數的無窮線性組合。左邊是這個線性組合的運算式,右邊是其影像。隨著項數的不斷增加,你可能會察覺到這個函數的樣子越來越熟悉,如果項數無窮,那麽它便成了e^x的泰勒級數!

這簡直讓人感到驚奇,畢竟e^x並不是一個多項式,如此一來,我們竟然得到了一個完全超越向量空間的東西!想一想,這就像收集無數石頭,不斷疊加,最後竟然莫名其妙地變成了一塊披薩,天南海北的聯想!那麽,這究竟是什麽問題呢?我認為值得深入探討,因為引入無窮的方式其實頗具微妙。在這裏,答案就在於「無窮」是一個概念,而並非具體的數值。對於任何有限的線性組合,是可以得到一個多項式的,因此屬於向量,無論這個組合有多龐大。然而,一旦項數趨近於無窮,極限結果就不再是一個多項式,這樣便超出我們的向量空間。

我喜歡用一個圖來解析這個問題,圖確實展示了我們向量空間所涵蓋的區域和邊界。線性組合的第一項給出的則是向量空間中的某個元素,隨著我們不斷添加更多項,線性組合逐漸推進到向量空間的邊界。而在無窮項的極限中,結果幾乎就處於向量空間的邊緣,接近外界。明白為何在向量空間中引入「無窮」是件風險性的事,的確非常重要。那麽,對量子向量空間意味什麽呢?
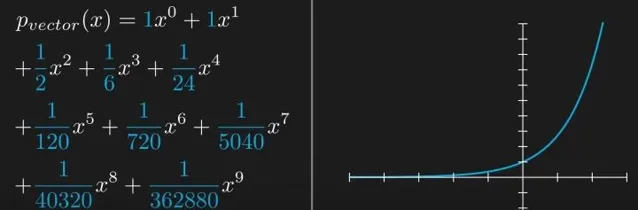
這意味著如果量子態處於結果態的無窮疊加之中,有可能這個量子態會超出向量空間,從而不再屬於量子態,這實在是個大麻煩!那麽,我們應當如何解決這個問題呢?這顯然是一個數學難題,我們可以在量子向量空間裏額外定義一個規則,以保證每個收斂的向量和都必須收斂到向量空間中的一個元素,這聽上去也許有些搞笑,但這確實是我們的權利。

你或許不敢相信,但我所描述的,實際上便是希爾伯特空間的真諦!希爾伯特空間的定義為具有內積並且完備的向量空間。接下來,我們來逐步剖析這些數學術語:內積其實是廣義的點積,具體內容會在後面的文章中介紹。完備性則意味著每個收斂的向量序列(像是無窮線性組合的部份和)都會收斂到向量空間內的某個元素。因此,希爾伯特空間就是一個內積下的向量空間,其中每個收斂的和或序列都能收斂到這個空間的某個元素——這幾乎與我們剛才添加的條件是等同的!

如果你希望對完備性有直觀理解,我們可以參考向量空間的圖示。在多項式向量空間中,我們把無窮線性組合視為位於空間邊緣的某點,希爾伯特空間則包羅這些邊緣,確保沒有任何空隙能讓無窮線性組合逃出空間。因此,在這個意義下,它是「完備」的,包含著所有可能的情況。盡管這個圖在數學上不夠嚴謹,但我認為它提供了良好的直觀理解。所以,希望你能意識到,在量子力學中運用希爾伯特空間是極為合理的;這只不過是我們使用無限維向量空間的一種方式,同時確保在將無窮多個態向量疊加時,絕不會得到荒謬的結果。我們的目標是,在進行線性組合的過程中,同樣能保持量子態的清晰,而不是收獲一塊不知道從哪裏來的披薩。從今天起,我們將把量子向量空間看作希爾伯特空間,通常使用這個符號來表示:所有的量子態都存在於此範圍之內。