牛頓所提出的萬有重力定律宛如一座巍峨聳立、不可撼動的豐碑,其重要性和影響力不言而喻,相信大家對其都不會感到陌生。通常情況下,我們將其核心內容理解為:任何兩個具有質素的物體之間必然存在重力,且重力的大小與它們的質素成正比,與它們之間距離的平方成反比。這一定律以其簡潔明了、深刻有力的形式,為我們揭開了宇宙中物體相互吸引這一基本規律的神秘面紗,成為人類理解天體運動、重力現象以及眾多相關領域的基石,對科學的發展和人類對自然界的認知起到了無可替代的推動作用。
然而,當我們懷著一顆好奇且探索的心,對這一定律進行更為深入和細致的思考時,一個饒有趣味卻又充滿挑戰的問題逐漸浮出水面:如果兩個物體之間的距離無限趨近於零,那麽它們之間的重力是否會如同脫韁的野馬一般趨向於無窮大?
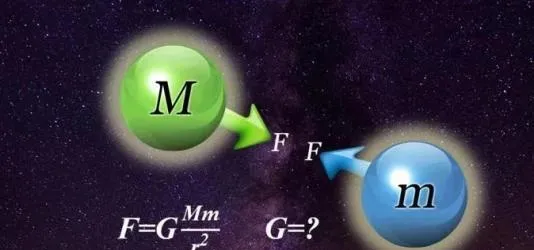
為了全面且深入地探討這個極具挑戰性的問題,讓我們首先重新審視萬有重力定律的數學運算式:「F = Gm1m2/r^2」。在這個公式中,F 代表著兩個物體之間所產生的重力,G 代表著重力常數,其數值約為 6.672 x 10^-11 N·m^2/kg^2,m1 和 m2 分別代表兩個物體各自的質素,而 r 則代表兩個物體之間的距離。從這個公式的表面形式進行簡單的推理和分析,如果 r 無限趨近於零,似乎直觀地可以得出結論,F 應當會無可阻擋地趨向於無窮大。

然而,當我們將目光從理論的公式轉向日常生活的實際經驗和觀察時,卻會發現一個令人深思的現象:這樣看似必然會出現的「重力無窮大」的奇異情況,在我們的日常生活中卻從未有過絲毫的蹤跡和跡象。我們常常將兩個物體緊密地靠攏、接觸甚至擠壓在一起,但卻從未目睹過任何類似於「重力無窮大」這樣超乎尋常的現象發生。這一現實與理論推理之間的明顯差異,不禁令人心生疑惑和困惑,進而引發我們對萬有重力定律的嚴謹性和普適性產生了深深的思考和質疑:難道這一被廣泛接受和尊崇的萬有重力定律存在著某種尚未被我們察覺和理解的缺陷或「bug」嗎?
為了更全面、更深入、更準確地探討和回答這個至關重要的問題,我們需要對萬有重力定律進行一種更為嚴謹、精確和深入的理解和詮釋。實際上,萬有重力定律應當被更加準確和完整地表述為:「任何兩個質點之間都存在透過其連心線方向上的相互吸引的力,其大小與它們質素的乘積成正比,與它們距離的平方成反比。」在此,我們需要特別關註和深入理解「質點」這一在物理學中具有特殊意義和重要地位的概念。
所謂質點,從物理學的定義和角度來看,是指一個具有質素但卻沒有體積的理想化的點。需要特別強調的是,這一概念僅僅是物理學為了簡化和處理某些復雜問題而構建和引入的一種理想化的模型,在現實世界的客觀存在中,這樣純粹的、沒有體積的點是決然不存在的。因為我們在現實生活中所能直接觀察和接觸到的任何具有質素的物體,無論其大小和形態如何,都是不可避免地具有一定的體積和空間占據。
所以,當我們真正具體地去討論和分析兩個具有實際物理意義和存在形式的物體之間的重力關系時,「兩個物體之間的距離」這一概念應當被更為準確和科學地定義為「兩個物體質心之間的距離」。為了更直觀和清晰地理解這一概念,讓我們透過一個具體的例子來進行闡述和說明。
假設有兩個半徑均為 5 厘米的實心鐵球。當我們嘗試將它們盡可能緊密地挨靠在一起時,即使在我們的操作中確保兩個鐵球之間沒有留下哪怕是一絲一毫的縫隙,它們質心之間的實際距離仍然會保持在 10 厘米左右。很顯然,這樣的距離狀況遠遠算不上是「距離無限趨近於零」的極端情況。
與此同時,我們還需要考慮到另一個重要的因素,那就是重力常數 G 的數值極其微小。由於這一極小的重力常數值的存在,即使在兩個物體的質素相對較大的情況下,它們之間的重力大小仍然會受到極大的限制和約束。就以我們所假設的這兩個半徑為 5 厘米的實心鐵球為例,由於它們質心之間的距離相對較大,再加上重力常數的微小,兩者共同作用的結果是這兩個鐵球之間所產生的重力極其微小,微小到在絕大多數的實際套用和分析中,都可以被合理地忽略不計,而不會對我們的研究和結論產生任何顯著的影響。
那麽,如果我們進一步假設,將這兩個鐵球的半徑不斷地進行縮小,試圖讓它們的質心盡可能地無限接近,在這種情況下,它們之間的重力是否就能夠如我們最初所推測的那樣趨向於無窮大呢?經過深入的分析和思考,我們會發現實際情況並非如此簡單和直接。
這是因為這兩個鐵球的質素與其體積之間存在著緊密且直接的比例關系,而它們的體積又與它們自身半徑的立方成正比。這一內在的數學關系和物理規律意味著,在我們不斷縮小鐵球半徑的過程中,萬有重力公式中的分母(即距離的平方,r^2)不可能縮小的速度比分子(即兩個物體質素的乘積,m1m2)更快。

為了更清晰地說明這一原理,讓我們透過一個具體的數值計算來進行展示和解釋。假設我們將這兩個鐵球的半徑縮小為原來的一半,那麽在萬有重力公式中的分母(r^2)將會縮小為原來的四分之一,而分子上所表示的兩個鐵球質素的乘積(m1m2),由於鐵球體積的縮小(與半徑的立方成正比),將會縮小到原來的六十四分之一。透過這樣直觀的數值對比和分析,我們可以清晰地看到,在這種情況下,根本不可能出現「重力無窮大」這樣極端和不符合實際物理規律的情況。
接下來,讓我們進一步深入探討和思考一個更為復雜和具有挑戰性的情況。假如我們在一個相對較大的鐵球的中間部位精心地挖掘出一個洞,然後將一個相對較小的鐵球放置在這個洞中,那麽在這種情況下,我們是否就能夠成功地實作讓大小兩個鐵球的質心之間的距離無限趨近於零,甚至達到直接重疊的理想狀態,從而使得它們之間的重力趨向於無窮大呢?經過嚴謹的物理分析和推理,我們會得出否定的答案。
這一結論的得出是基於高斯定理的深刻原理和推導。根據高斯定理可以精確地推匯出,在一個半徑為 R 的球體內部,當我們考慮距離球心為 r 的某一特定位置時,可以合理地認為這個位置僅僅會受到來自這個球體半徑為 r 這部份質素所產生的重力作用,而 r 到 R 這部份「球殼」的質素所產生的重力,其合力在數學和物理上被證明為零。
由此我們可以清晰地推斷和理解,如果我們真的在一個大鐵球的質心位置巧妙地挖掘出一個洞,然後將一個小鐵球準確地放置在這個特定的位置,那麽它們之間所產生的重力並不會如同我們最初的直覺和推測那樣趨向於無窮大。相反,當大小兩個鐵球的質心完全重疊在一起時,由於上述的物理原理和規律,它們之間的重力不但不會趨向於無窮大,反而會出人意料地減小為零。
看到這裏,可能會有一些思維敏銳且充滿探索精神的讀者進一步提出一個更加深入和具有挑戰性的疑問:假如我們能夠在確保兩個鐵球質素始終保持不變的前提條件下,不斷地運用各種可能的手段和方法來壓縮這兩個鐵球的半徑,進而有效地使它們質心之間的距離無限趨近於零,在這樣一種極端且理想化的情況下,總應該能夠成功地實作讓它們之間的重力趨向於無窮大的預期目標了吧?對於這個極具挑戰性和前瞻性的問題,愛因斯坦所提出的【廣義相對論】為我們提供了一種全新的、更為深刻和全面的思考視角和理論框架。
根據愛因斯坦提出的具有開創性和革命性的【廣義相對論】,我們可以透過嚴謹的理論推導得出一個重要的結論:對於任何具有質素的物體而言,只要其自身的自然半徑被壓縮到小於或等於一個特定的臨界值,這個物體就會不可避免地轉化成為一個極其特殊和神秘的天體——黑洞。這個在理論上具有關鍵意義的特定臨界值被科學界賦予了一個專門的名稱——「史瓦西半徑」。
值得我們特別關註和深入思考的是,與我們日常生活中所常見的物體的自然半徑相比,「史瓦西半徑」的數值實際上是極其微小的。例如,我們所熟悉的地球,其「史瓦西半徑」大約僅僅為 9 毫米。這一微小的數值與地球實際的半徑相比,簡直是微不足道。
這也就意味著,如果我們真的擁有超越想象的能力和技術手段,能夠在質素保持恒定不變的前提條件下不斷地對這兩個鐵球進行極度的壓縮,使其半徑不斷縮小並最終突破「史瓦西半徑」的限制,那麽這兩個鐵球就會無可避免地轉化成為兩個極其微小但卻具有極其強大重力場的黑洞。
而根據【廣義相對論】對黑洞這一神秘天體的深刻描述和理論分析,在黑洞的中心位置存在著一個被稱為「奇異點」的特殊區域。這個「奇異點」具有令人難以置信的奇異性質,其體積被理論推測為無限小,而密度則被認為是無限大。

因此,從純粹的理論推導和數學計算的角度出發,我們根據萬有重力定律可以大膽地推測,如果我們能夠成功地讓這兩個黑洞的「奇異點」之間的距離無限趨近於零,那麽它們之間的重力將會無可阻擋地趨向於無窮大。
然而,我們絕對不能僅僅因為這樣的理論推測和數學計算結果,就草率地認為萬有重力定律本身存在著某種內在的錯誤、缺陷或者不完整性。相反,我們應當以一種更加客觀、全面和深刻的視角來認識和理解這一現象。實際上,我們應當清醒地認識到,萬有重力定律如同其他任何科學理論一樣,不可避免地存在著自身特定的適用範圍和局限性。
黑洞的「奇異點」這一極端的物理概念和現象,已經遠遠超出了萬有重力定律原本所設定和涵蓋的適用範圍。實際上,不僅僅是萬有重力定律,在當前的科學研究和理論體系中,任何一種科學理論都不可避免地具有自身的適用邊界和局限性。
對於黑洞的「奇異點」這一極其特殊和神秘的物理現象,目前我們所擁有的所有已知的物理理論和定律實際上都無法給出完全準確、全面和令人滿意的描述和解釋。這也正是為什麽在物理學界存在著這樣一種被廣泛認同和接受的觀點和說法:在黑洞的「奇異點」處,所有已知的、基於傳統物理理論和定律所建立起來的物理規律和模式都會不可避免地失去其有效性和適用性。

為了更全面、更深入地理解萬有重力定律的局限性以及黑洞這一神秘天體所具有的奇異性質,我們有必要進一步探討和研究物理學中的一些基本概念、原理和理論體系。
在傳統的經典物理學框架中,我們通常基於一系列基本的假設和前提來構建我們的理論模型和物理規律。其中一個重要的假設就是認為物體的質素是一個恒定不變的物理量,並且空間和時間被視為絕對的、獨立的物理量,不受物體的運動狀態和相互作用的影響。
然而,隨著科學研究的不斷深入和理論的不斷發展,特別是愛因斯坦的相對論的提出和建立,我們對質素、空間和時間等基本物理概念的理解發生了根本性的變革和昇華。
根據相對論的核心觀點和理論體系,質素和能量不再被視為兩個完全獨立和無關的物理量,而是透過著名的質能方程式 E=mc^2 建立起了內在的、深刻的聯系和等價關系。

同時,相對論還革命性地提出了空間和時間不再是絕對不變的,而是相互關聯、相互影響的,並且會隨著物體的運動狀態而發生相對的變化和扭曲。這種對空間、時間和質素等基本物理概念的全新理解和詮釋,在處理涉及高速運動、強重力場等極端物理情況和現象時,展現出了比傳統的經典物理學更為準確、全面和深刻的理論優勢和預測能力。
黑洞作為一種在宇宙中極其特殊和極端的天體現象,其內部的重力場強度達到了令人難以置信的程度,時空的彎曲和扭曲也達到了前所未有的極端水平。
在這種極端的物理環境下,傳統的基於牛頓萬有重力定律的理論框架和物理模型已經無法準確地描述和解釋黑洞內部所發生的各種奇特物理現象和過程。
從量子力學的角度來看,當我們試圖深入研究和理解微觀尺度下的物理世界時,同樣會發現萬有重力定律存在著明顯的局限性和不適用性。
量子力學的核心理論和基本原理揭示了微觀粒子所具有的獨特性質和行為模式,例如波粒二象性、不確定性原理等。這些與我們在宏觀世界中基於經典物理學所形成的直覺和經驗有著極大的差異和沖突。

然而,到目前為止,盡管科學界進行了大量的研究和嘗試,但仍然尚未成功構建出一個能夠將重力與量子力學完美統一和融合的成熟理論框架。
對於黑洞的研究,其復雜性和深度遠遠超出了單一學科和單一理論的範疇。它不僅涉及到重力理論這一核心領域,還與熱力學、消息理論等多個看似不同但又相互關聯的學科領域有著密切的交叉和融合。
例如,黑洞的熵這一概念的提出,為我們理解黑洞的熱力學性質和演化過程提供了全新的視角和理論工具;而霍金輻射的發現和研究,則進一步豐富和深化了我們對黑洞與周圍環境相互作用以及其能量和物質交換過程的認識和理解。
回到我們最初所討論的萬有重力定律,盡管在處理大多數日常可見的、宏觀尺度下的重力現象和問題時,它表現出了極高的準確性和實用性,但當我們面對諸如黑洞「奇異點」這樣極端和特殊的物理情況時,我們必須認識到其固有的局限性和不足之處,並尋求更高級、更全面、更精確的理論來進行描述、解釋和預測。











