在工程學和物理學領域,許多復雜系統的動態特性,即其動力學,可以透過向量和張量的數學語言來精確和優雅地表達。向量在這裏用來描述具有明確大小和方向的物理量,比如速度和力,它們在數學上表示為一維陣列,每個元素對應一個維度或方向。張量則是向量的高維擴充套件,它們是更復雜的數學物件,能夠表示多維空間中的關系,例如應力、應變或慣性等。

在講述向量時,這裏的指代不是指具有明確方向和大小的傳統幾何向量,而是指更廣義的數學上的向量概念。 數學中的向量是一個元素序列或陣列,這些元素可能是數碼、符號,或者更復雜的結構,並不一定與物理空間中的方向和大小有直接聯系。 文章從這種廣義的向量出發,進一步探索張量的概念,張量是一種更高維度的數學物件,能表達多維空間中的復雜關系。然而,為了使概念更易於理解,這種討論可能會簡化一些數學上的復雜性和嚴謹性。
什麽是向量?
向量是一個集合中的元素。這個集合稱為 向量空間( Vector space ) 。為了使一個集合有資格成為向量空間,它需要滿足某些條件。簡單說,一個向量空間 V 在一個 純量域 F上是一個集合,對這個集合定義了加法和純量乘法運算,具有以下內容:
基集
基集是向量空間中的一組特殊向量,它們的特點在於向量空間中的任何向量都可以透過這些基向量的線性組合來表示。這種線性組合是透過將每個基向量乘以一個純量(數碼)然後將它們相加來實作的。在向量空間V中的每個向量都可以唯一地表示為這些基向量的和。值得註意的是,對於同一個向量空間,可以有多種不同的基集,每種基集都能以唯一的方式表示空間中的所有向量,盡管具體的基向量可能不同。

註意純量倍數是上標,而基是下標。這是物理學中的標準記號。在愛因斯坦求和約定中,我們省略求和符號:

在數學運算式中,如果一個索引(比如一個字母)同時作為上標和下標出現,這表示對該索引進行求和運算,涵蓋了該索引的所有可能值。這種索引被稱為啞指數。假設我們有一個三維向量空間,並選擇了一個基集,包括三個基向量 e_1, e_2, 和 e_3。現在,我們有一個向量 v 在這個空間中,它可以用這個基集來表示。
向量 v 的分量可以用 v¹, v², v³ 來表示,這些分量是與基向量 e_1, e_2, 和 e_3相對應的純量倍數。
現在,讓我們用這些分量來表達向量 v。在不使用愛因斯坦求和約定的情況下,向量 v 的表示為:
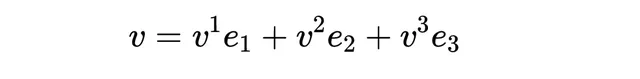
這裏,v¹, v², 和 v³ 是向量 v 在基向量 e_1, e_2, 和 e_3 方向上的分量。
但是,如果我們套用愛因斯坦求和約定,我們不需要顯式地寫出求和符號。我們只需寫出每個分量和對應基向量的乘積,並預設所有具有重復索引的項都會被求和。這樣,向量 v 的表示就變成了:
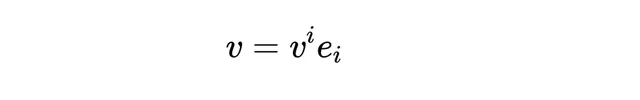
在這個運算式中,i 是一個啞指數,它在這個運算式中重復出現了(一次作為上標,一次作為下標)。根據愛因斯坦求和約定,這意味著我們將對 i 的所有可能值進行求和,即 i = 1, 2, 3。因此,這個運算式隱含了上面提到的完整求和過程,即:
通常將向量分量表示為列。

向量空間的維度
向量空間的維度是所需的基向量的最少數量。
向量空間之間的對映
在兩個向量空間U和V之間,存在一種對映M,它定義了一種特定的方式,將U空間中的每一個向量轉換為V空間中的一個對應向量。這個過程意味著對映M接受U空間中的向量作為輸入,並根據某種規則,產生V空間中的一個對應向量作為輸出。這種對映是系統性的,確保U空間中的每個向量都能找到一個與之對應的V空間中的向量。
假設 U 是一個二維向量空間,其中的向量可以表示為 (u1, u2) 的形式,其中 u1 和 u2 是實數。V 是一個三維向量空間,其中的向量表示為 (v1, v2, v3)。
現在,我們定義一個對映 M,它將 U 空間中的每個向量轉換為 V 空間中的一個向量。例如,我們可以定義對映 M 如下:
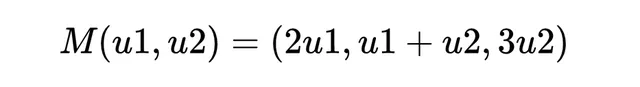
這意味著,對於 U 空間中的任何向量 (u1, u2),對映 M 會產生 V 空間中的向量 (2u1, u1 + u2, 3u2)。
線性對映是一種也遵守以下性質的對映:

在定義線性對映時,需要確保兩個向量空間 U 和 V 都基於同一個數學結構,即同一個域F,這樣在這兩個空間中的運算才能保持一致性。這個域F可以是實數集或復數集等,提供了加法、減法、乘法和除法運算的基礎。
線性對映之所以有用,是因為它保持了向量的加法和純量乘法結構不變。 這意味著,只需知道向量空間的基向量在對映下的結果,就可以確定任何向量在該對映下的結果。這是因為向量空間中的任何向量都可以表示為基向量的線性組合 ,因此,一旦基向量的對映結果已知,就可以透過相應的線性組合計算出任何向量的對映結果。
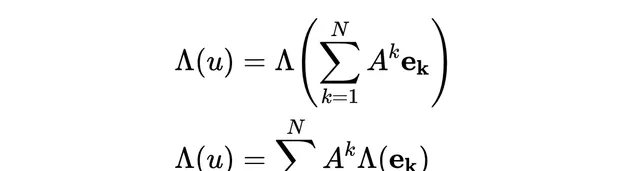
由於 每個域F也是一個向量空間 ,我們可以定義將向量空間V對映到域F的向量空間F的對映。正式地:
所有這些線性對映的集合被稱為 對偶空間( Dual Space ) ,通常表示為。

對偶空間自然是一個向量空間,因為可以定義加法和純量乘法運算:
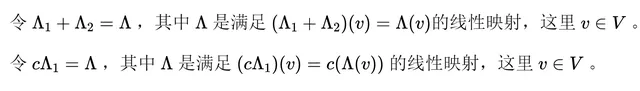
因此,對偶空間的元素通常被稱為 協向量( covector ) 或對偶向量。
對偶空間有時也被稱為代數對偶空間。
由於線性對映完全由其在基向量上的作用決定,對偶向量空間將具有與 V 相同的維度。也就是說,每個協向量都可以表示為:

對於協向量,請註意純量倍數是下標,而基是上標,與向量的常規相反 。 這種索引運算將使處理向量空間和尚未定義的張量變得容易。 協向量通常用行矩陣的分量表示。

常見的符號
在進一步進行之前,我們需要改進我們的符號。我們通常不使用 () 來表示協向量對向量的作用。相反,我們通常使用:

這是量子力學中常用的狄拉克符號(Dirac notation),也稱為「量子力學的概率符號」,用於描述量子態和量子力學運算。這種符號非常緊湊且表達能力強,適用於處理復雜的量子系統。
向量也是對映
我們知道:
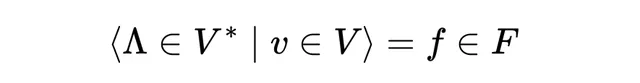
如果我們取整個向量空間V,並保持協向量不變,輸出是由F中元素組成的子集。

相反,如果我們取整個對偶向量空間V*,並保持向量不變,輸出再次是由F中元素組成的子集。
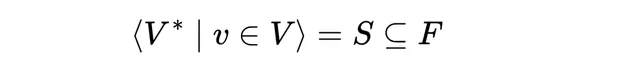
本質上,協向量將V對映到F

而向量可以理解為從V*到F的對映

如果向量空間的維數是有限的,對偶空間的對偶就是原始向量空間。
如何為對偶空間選擇基?
如前所述,我們可以為向量空間選擇任何基。但對偶空間V*不是任何向量空間,而是與定義良好的向量空間V緊密相關的東西。因此,為了使計算更容易,選擇基時應該:

需要強調的是,基向量eᵏ和對偶空間中的基向量eₖ雖然在記號上相似,但它們之間並沒有直接的對應關系。將eᵏ和eₖ視為彼此的對偶是不準確的。使用這種記號,計算起來相當簡單:

什麽是張量?
總結到目前為止的學習,
那麽做這樣的對映呢?
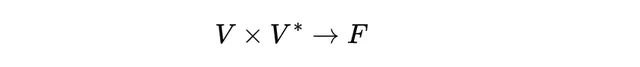
其中x表示集合的笛卡爾積。 或者更好:
這種在每個輸入中都是線性的(多線性)對映被稱為張量。
張量是一種數學物件,它被定義為在每個輸入上都保持線性的多線性對映。這意味著如果一個對映接收多個輸入,它會對每一個輸入獨立地保持加法和純量乘法的線性。張量能夠處理多個向量作為輸入,並且對每個輸入向量都執行線性運算,使其成為描述多維空間中復雜數據和關系的有力工具。
它按照一定順序接收一堆向量和協向量,並產生F中的一個元素。即:
張量積
透過稱為張量積的運算,可以從單個向量和協向量構造張量。例如:
圓圈中的 x 表示張量積。上述範例張量需要按順序(協向量,向量)輸入。
張量如何對參數運算?
為了得到結果,考慮使用向量和協向量構造的張量:
為了計算其對某個輸入的輸出,我們可以分別乘以輸出。
同時,
然後,
總共有 N x N 項在求和中。 從上述計算中也很明顯:
因此,張量 T 由 N x N 項特征化。通常的慣例是用矩陣表示需要2個輸入的張量的分量。
一般來說,一個張量將有 Nʳ 個分量來表征它,其中 r 是輸入的數量。
還應該強調,並非所有張量都可以透過組合向量和協向量來構造。
有一個常見的誤解認為矩陣是二階張量。矩陣只是表示在固定基集後二階張量的純量倍數的一種方式。實際上,適當域上 M X N 維矩陣的集合形成一個向量空間。
通常,在表示張量時我們會省略基向量和求和符號:
透過觀察指數的位置,很明顯張量運算的物件類別以及運算的順序。復雜的張量通常會有更多的指數,如:
具有相同形式的張量屬於一個稱為 張量積空間 (TSP)的集合。TSP 本身是向量空間,其中透過它們對輸入的作用來定義加法,類似於對偶空間定義加法的方式。
張量的秩
如果張量的形式是:
即,它接受 P 個協向量和 Q 個向量作為輸入,那麽它被稱為秩為 (P, Q) 的張量。張量的階只是 P+Q。
由於向量接受 (1 個協向量,0 個向量) 的輸入,因此向量是秩為 (1,0) 的張量。 同樣,協向量接受 (0 個協向量,1 個向量) 的輸入。所以協向量是秩為 (0,1) 的張量。 此外,域F 的元素不需要任何 (#協向量,#向量) 的輸入就可以生成域F的元素。 在這個意義上,純量是一個秩為 (0,0) 的張量。
降低張量的秩
考慮一個秩為 (5,3) 的張量。如果我們給它4個協向量和1個向量,那麽它就在等待獲取 1 個協向量和2個向量。 由於秩為(1,2)的張量接受1個協向量和2個向量,上述運算生成了一個秩為 (1,2) 的張量。
因此,我們可以透過給它一些(協向量,向量)來生成一個秩較低的新張量。











