什麽是嵌入?
嵌入是將某些數據物件表示為向量,構造為將數據物件的某些內容編碼為其向量表示的幾何內容。
這非常抽象,但並不像聽起來那麽復雜。
首先,我們需要介紹一點(非常少)數學。向量是兩個聽起來不同但實際上相同的東西:
- 向量是多維空間中的一個點。
- 向量是純量值的有序列表,即數碼。
要了解這是如何工作的,請考慮兩個數碼的列表。例如,$(6,4)$和$(2,8)$。您可以看到我們可以將它們視為x-y軸上的座標,每個列表對應於二維空間中的一個點:
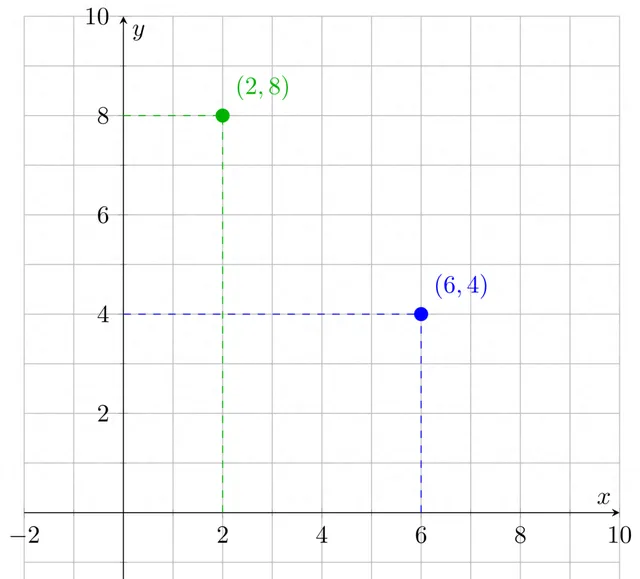
如果我們有三個數碼,比如$(3,2,5)$和$(4,5,2)$,那麽這對應於三維空間中的點:
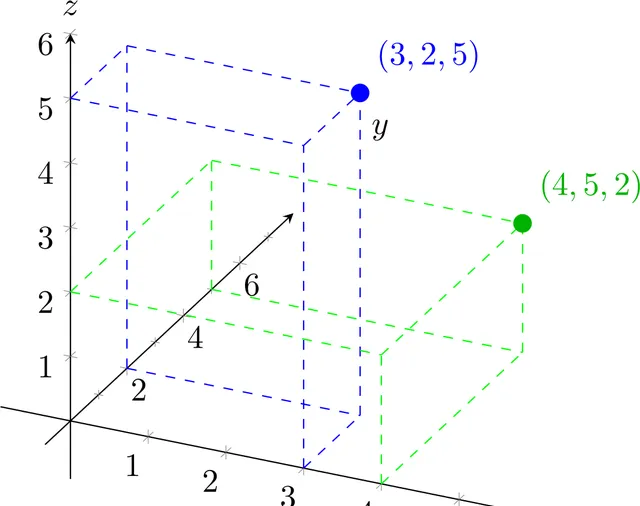
重要的是,我們可以把它擴充套件到更多的維度:4,5,100,1000,甚至數百萬或數十億。繪制一個有一千個維度的空間是非常困難的,想象一個維度幾乎是不可能的,但是從數學上講,這真的很容易。
例如,點$(6,4)$和$(2,8)$之間的距離只是畢達哥拉斯定理的套用。給定兩點$a=(x_1,y_1)$和$b=(x_2,y_2)$,它們之間的距離是:
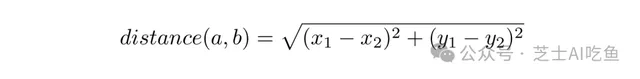
對於$(6,4)$和$(2,8)$,這意味著:
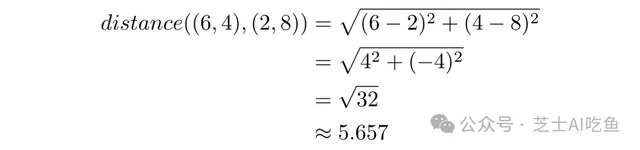
對於三維,我們只需透過添加一項來擴充套件公式。對於$a=(3,2,5)$和$b=(4,5,2)$:
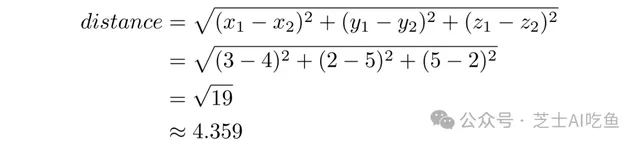
我們可以將這個公式擴充套件到任意維數的向量。我們只是添加更多的術語,就像我們從二維到三維一樣。
除了距離,我們在高維向量空間中使用的另一個度量是兩個向量之間夾角的余弦。如果您不僅將每個向量視為一個點,還將其視為距離原點的一條線(由向量$(0,0,0,…)$指定的點),那麽您可以計算兩個向量之間的夾角(下圖中為$\θ$)。
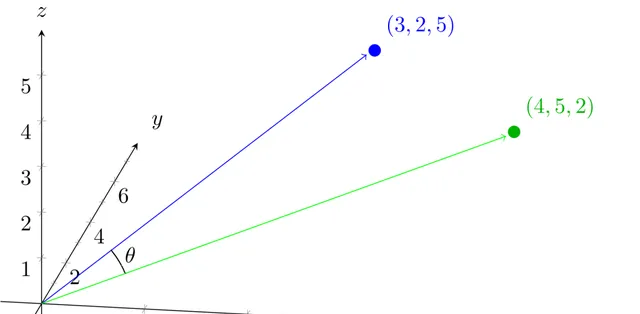
為了計算這個,我們有另一個公式,可以擴充套件到任意數量的維度。我們知道向量$a$和$b$之間角度$\θ$的余弦是:
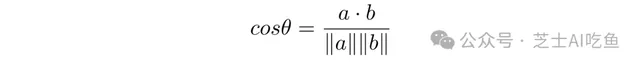
這比看起來要復雜,但不多。$a\cdot b$稱為兩個向量的點積,很容易計算。如果$a=(3,2,5)$和$b=(4,5,2)$,那麽:
至於$||a||$和$||b||$,它們是向量的長度,即從原點到該點的距離。所以:
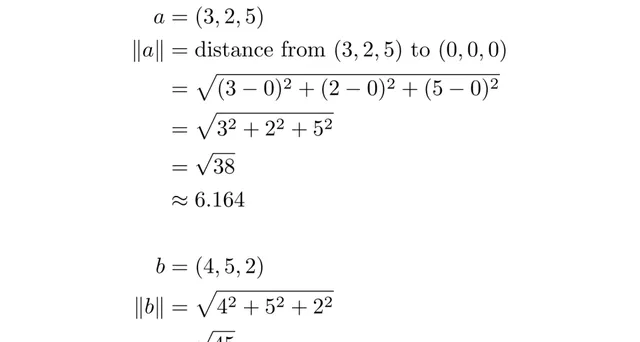
因此,要計算$cos\theta$:
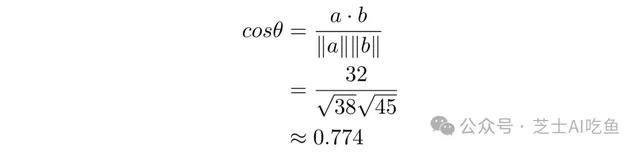
這個余弦對應於大約39.3°的角度,但是在機器學習中,我們通常在計算余弦後停止,因為如果兩個向量中的所有數碼都大於零,那麽余弦的角度將在0和1之間。
這看起來像很多數學,但是如果你仔細看,你會發現它只是加法、減法、乘法、除法、一個指數和一個平方根。簡單但無聊和重復的東西。你實際上不必做任何數學運算。我們讓電腦在身邊的全部原因就是為了做這種事情。但是你應該明白向量是數碼列表,理解使用向量的概念,理解如何,不管向量有多少維,我們仍然可以做計算距離和角度之類的事情。
讓這一點如此重要的是,我們保存在電腦上的任何數據也只是一個數碼列表。如果我們選擇這樣看待它,每一個數據項——數碼圖片、文本、錄音、3D模型檔,任何你能想到的可以放入電腦檔的東西——都是一個向量。
我們如何為事物分配嵌入向量?
嵌入的目的是為數據物件分配向量,以便它們在高維空間中的位置編碼關於它們的有用資訊。如果我們選擇以這種方式看待數據物件——文本、影像或我們正在處理的任何其他東西——它們已經是向量了。這些向量的位置並沒有告訴我們任何關於它們的有用資訊。
考慮這四個影像:

每個都是用標準RGB調色盤著色的450x450像素影像。這意味著圖片由202,500個像素組成,每個像素的紅色、綠色和藍色值在0到255之間有一個數碼。將其轉換為具有607,500個維度的向量是微不足道的。
我們可以拍攝任何一對影像,計算它們之間的距離或測量它們的余弦,但是蘋果之間不太可能特別近或者離橘子特別遠。至少,如果我們使用數百張蘋果和橘子的照片,而不僅僅是四張,那就不太可能了。
更有可能的是,我們會得到這樣的東西:
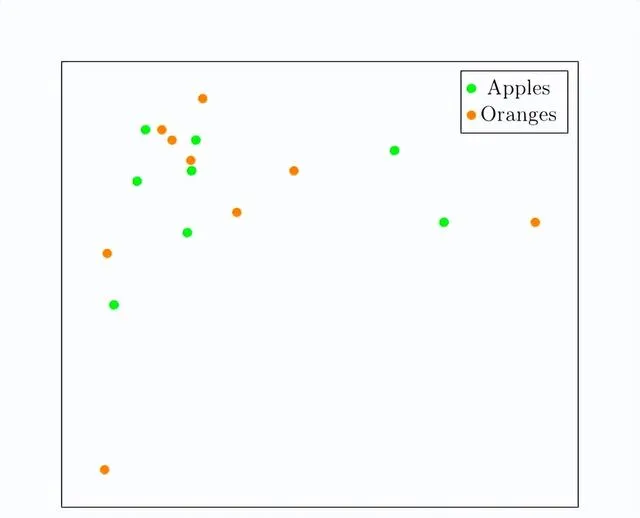
我們無法在60萬個維度上畫圖,所以這張圖只用了兩個維度來證明這一點:我們應該預期蘋果和橘子是半隨機放置並混合在一起的。
我們希望為每個影像分配一個獨特的嵌入,使得蘋果靠近橘子,反之亦然。我們想要這樣的東西:
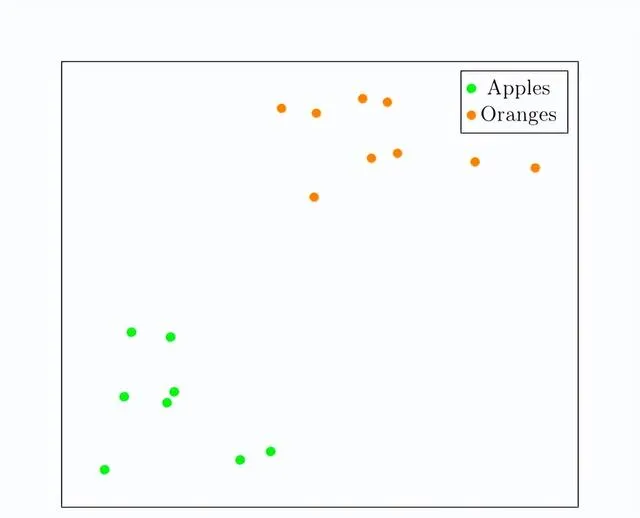
為此,我們構建了一個神經網絡(我們稱之為嵌入模型),它將607,500個維度向量作為輸入,並輸出一些其他向量,通常維度較少。例如,廣泛使用的ViT-B-32影像嵌入模型將輸入影像轉換為512維嵌入向量。
然後我們用蘋果和橙子的標註圖片訓練嵌入模型,指示它慢慢調整網絡的權重,以分離蘋果和橙子的嵌入向量。經過多次迴圈訓練,我們期望當我們給蘋果的模型圖片作為輸入時,它會輸出彼此之間的距離比我們給它橙子圖片作為輸入時得到的向量更近的向量。
這些輸出向量被嵌入,它們共同形成一個嵌入空間。單個嵌入的位置編碼了有關其相應數據物件的有用資訊:在這種情況下,某物是蘋果還是橘子的圖片。
區分蘋果和橘子是一個非常簡單的場景,但是你可以很容易地想象把它標定為許多功能。
在一些用例中,我們甚至可以在沒有明確說明哪些特征相關的地方構建嵌入,我們讓神經網絡在訓練過程中弄清楚。例如,我們可以透過拍攝人臉來構建臉部辨識系統,並訓練嵌入模型輸出嵌入,將同一個人的照片靠近在一起。我們然後可以以他們的嵌入向量為鍵構建人們圖片的數據庫。
我們期望儲存的面透過嵌入空間分布:

我們可能會期望這個嵌入空間會編碼許多我們從未明確訓練過的特征。例如,它可能會將男性與女性隔離開來:
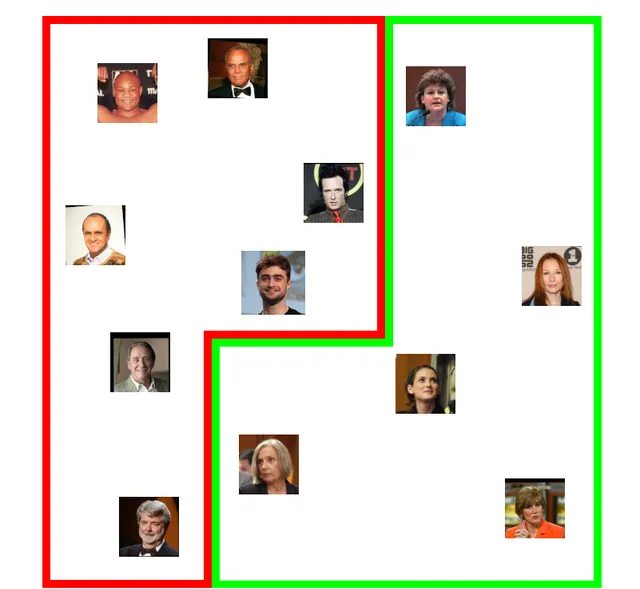
或者我們可能會發現人們根據頭發的特征聚集在一起,比如禿頂或灰色:
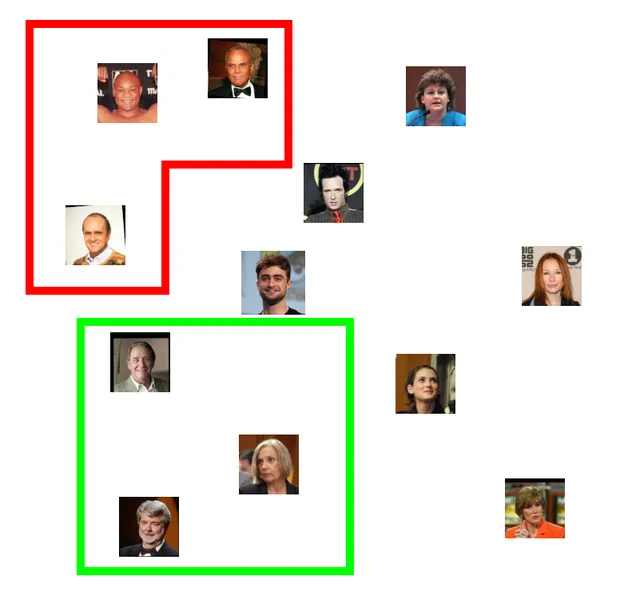
但是我們會期望,如果我們給它數據庫中某人的另一張照片,新照片的嵌入將更接近我們儲存的那個人的照片,而不是其他任何人:
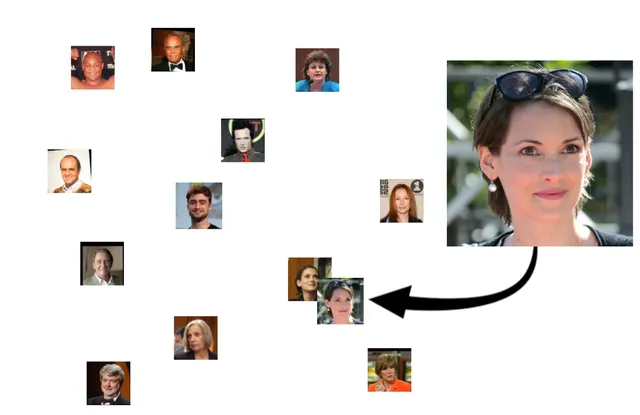
當然,它也會找到看起來相似的人,盡管我們希望他們不會像兩個實際上是一樣的人那樣親密:
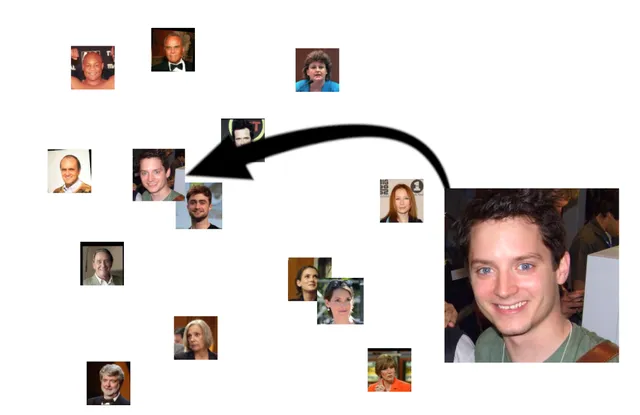
這突出了嵌入空間的邏輯:輸入是多種多樣的,但是透過將它們轉化為嵌入,我們將特征——有時是復雜的、隱藏的、微妙的或不明顯的特征——轉化為軟件可以輕松辨識的幾何內容。
嵌入空間還可以支持多種輸入類別,如文本和影像,建立通用嵌入空間並使您能夠在兩者之間進行對映。
例如,如果我們有一個帶有描述性標題的圖片數據庫,我們可以共同訓練兩個嵌入模型——一個用於影像,一個用於文本——在同一個嵌入空間中輸出向量。結果是影像描述的嵌入和影像本身的嵌入將彼此靠近。
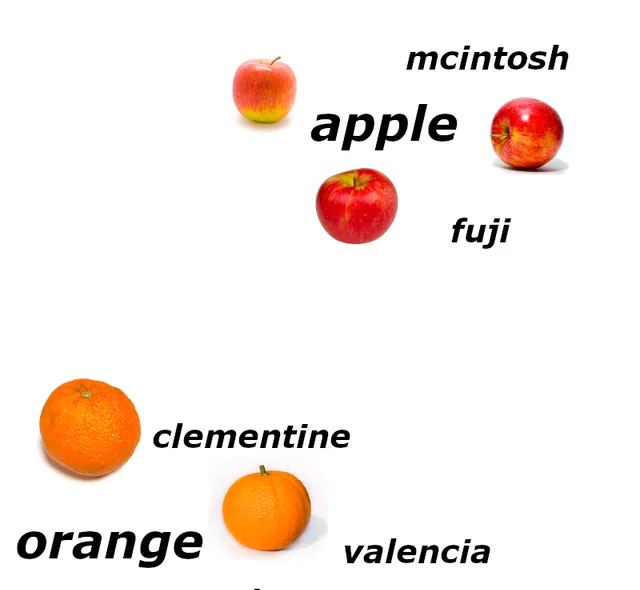
原則上,任何類別的數碼數據都可以作為建立嵌入的輸入,任何配對的數據類別——不僅僅是文本和影像——都可以用於建立多模式聯合嵌入空間。
嵌入有什麽好處?
就像瑞士軍刀一樣,問題應該是,它們有什麽不好?
我們已經展示了如何將嵌入用於影像分類和臉部辨識系統,但這還遠遠沒有用盡可能性。例如,從文本描述(又名「人工智能藝術」)中生成人工智能影像首先為文本和影像構建一個聯合嵌入空間,然後,當使用者輸入文本時,它會計算文本的嵌入,並嘗試構建一個將產生附近嵌入的影像。
嵌入是如此普遍有用,以至於它們可以在人工智能和機器學習中看到應用程式。任何需要相似性/不相似性評估、依賴隱藏或不明顯特征或需要不同輸入和輸出之間隱式上下文相關對映的應用程式,都可能以某種形式使用嵌入。
嵌入是現代機器學習和人工智能的一項重要技術,以某種形式出現在人工智能應用程式的範圍內。正確理解和掌握這項技術使您能夠利用人工智能模型為您的業務增加最大價值。
嵌入背後的理論甚至並不復雜:它只涉及從數據物件到高維向量空間中具有共同內容的點的對映,這些內容對你很重要。使用它們只是測量向量距離和余弦的問題,這是計算上微不足道的數學!
不幸的是,構建和訓練嵌入模型的實踐比使用它們更復雜。
英文原文連結
https://jina.ai/news/embeddings-the-swiss-army-knife-of-ai/











