文/老余
只要持續不斷的觀察所有事件,直到天荒地老,則世界上所有事物都會以固定的比例發生,如果發生了讓人意外的事件,人們會把這起事件認定為既定的宿命。
——雅各布·白努利
數學,是很多人的噩夢。
按道理,我們上學的目的之一是要培養對知識的興趣,但結果好像恰恰相反,學前班的孩子對知識各種好奇,有十萬個為什麽,而高考完的那一刻滿地都是被撕毀的書籍,被特別照顧的就是數學書。
但這並不是你的錯,也不是數學的錯,而是數學老師或者說是應試的問題。我們作為理性人,不能因為別人的錯而放棄學習、運用數學。
因為無論你喜不喜歡它,這個世界的底層執行邏輯,就是數學。
這是規律,不以任何人的意誌為轉移。
本文【數學思維的妙處】這個系列的第17篇,我們來討論下「大數定律」,這個定律對我的影響很大,希望對你也有用處。

一、什麽是大數定律?
這是概率論中的一個基本定理,說的是:當一個實驗隨著重復的次數越來越多,實驗結果的頻率(或者叫次數)會趨向於某個常數值,這個常數值就是事件發生的概率。
不夠通俗,舉個例子:
比如拋硬幣,我們知道每次落定後正反面朝上的概率是各50%,如果只拋10次,基本不會出現正反面各5次朝上的情況(理論上的各50%)。
雖然每次哪一面朝上是隨機的、是偶然的、是不可預測的、是我們無法控制的,但隨著實驗的次數越來越多,最終統計的結果是正、反面朝上的次數(頻率)就會越趨(收斂)近於各50%。
——短期看是隨機的,長期看是確定的,這就是大數定理。
1713年,雅各布·白努利(就是那個著名的白努利實驗的白努利)在數學上證明了「大數定理」,當我看到這個年份,其實有些意外,人類對很多數學概念啟蒙的很早,比如畢達哥拉斯定理,但唯獨在概率或者說在隨機這件事上,是很晚熟的,可見人類是多麽不習慣隨機。
就這麽一個定理,能給我們什麽啟發?
其實很深刻。
我們接著聊。

(二)大數定理與命運
我們總感嘆人生無常或者命運註定,人的命運真是註定的嗎?
看上去確實如此,不然為何那麽多文藝作品總是把「改天換命」作為主題呢,「我命由我不由天」這句台詞,不也引起了無數人的共鳴嘛。
這起碼說明了兩件事:
改命難嗎?
難!
沒有數學之前,我們連命運的定義都無法統一,你看幾千年來,用文學語言來解釋、闡述命運而寫成的書、編成的戲何止車載鬥量。
我們從這些海量作品中學到的,也不過是四點:遇貴人、站對隊、堅持住和運氣好,但這些都是因人因時因地而異,不具有普遍性。所以你看時頭頭是道,做時一腦懵逼。
但用數學的語言來描述,命運其實很簡單,其實就四個字——大數定律。
怎麽說?
白努利證明大數定律是偉大的,有意思的是他在證明的手稿邊上寫了一段話:
只要持續不斷的觀察所有事件,直到天荒地老,則世界上所有事物都會以固定的比例發生,如果發生了讓人意外的事件,人們會把這起事件認定為既定的宿命。
所以,命是什麽?是我們人生中的一次次選擇,就像那一次次拋在空中的硬幣,運是什麽?是我們一次次選擇後拼成的結果。
命運,就是我們一輩子所有選擇的集合。大數定理,是命運的數學原理。
知道了這些又有什麽用呢?
有大用!
因為,我們借此可以主宰自己的命運,可以「我命由我不由天」了。

(三)大數定理,如何指導現實生活?
我看到了兩點:
1、大數定理,能減少了我們的精神內耗
這個時代選擇很多,這是好事,選擇更多意味著我們可以「樹挪死,人挪活」,可以此處不留爺自有留爺處。
但選擇多也是壞事,這會讓我們頻繁挪、頻繁去別處。而一個人的時間和精力是有限的,頻繁的挪,你怎麽可能和原本就在這個行業浸淫的小夥伴競爭?
這正印證我小時候的印象較深的這幅挖水的漫畫。

我們很多時候之所以打幾槍換一個地方,到處去找所謂的風口,大概率是因為不了解「大數定理」:
——在一個行業裏深耕,我們才有機會在這個行業裏「拋硬幣」,只有一次次去拋,只要拋的次數足夠多,頻率就會收斂於概率,你期盼的結果才大概率會出現。
這是定律,與你是否高明動作是否優雅無關。
你看,絕大多數人為何一輩子碌碌無為?
或許不是因為不夠聰慧,而是過於聰慧,剛上這張桌拋了幾次沒有得到想要的,就已經在去找別的桌子的路上了。
他自己的理解可能不是努力的時長不夠,而是之前選的方向錯了,於是成了那個挖井水的人,到處挖,忙得不可開交,過年連家人都沒時間陪,但我們知道,他就是漫畫裏挖水的那個人,註定得不到想要的結果。
這是第一點,既然已經選了這個行業,且這個行業沒有被淘汰,那就堅定信心往前走,隨著「拋硬幣」的次數越來越多,頻次必然越來越接近於固有概率。
即使這個行業整體沈沒了,我們的選擇也要與之前的沈澱有相關性,千萬別相信什麽「心若在夢就在,只不過是從頭再來!」
那是歌詞,不是現實,你讓劉歡從頭來一次試試?凡是歌裏提倡的,都是有坑的,都是希望你來填的,別犯傻。

2、大數定理告訴我,何事驚慌?
我們來做個遊戲:
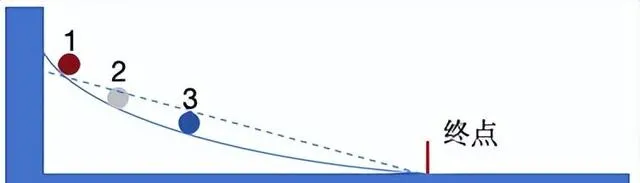
下面斜坡上高低不同的位置有三個球,分別滾下,滾到右側平面的終點用時最短即獲勝,你覺得哪個球會贏得比賽?

表面上看,3號藍色因為離終點最近,所以直覺上3號應該贏得比賽,但實際情況是,只要這個斜坡是「等時曲線」,1、2、3號到達終點的時間是一樣的。
註:在「等時曲線」上,不同位置的球到達終點的時間一樣,由荷蘭數學家惠更新在1673年發現。
等時曲線還有一個特性,就是球從這條曲線的這個點滾下去,比其他任何曲線和直線滾下去的時間,都最短的。
比如1號球,從同等高度的等時曲線(實線)往下滾,就比從直線(虛線)上滾到終點用時少。
那這個時間是多少呢?
直接給答案,t=π ,你看,「π和g」(g是重力加速度)都是常數,所以時間只與「r」有關。
這意味著,只要這個球在這條賽道的「等時曲線」上,無論它從哪個位置、什麽高度出發,他到達終點的用時是最短的。
這和我們的職場賽道是一樣一樣的,當我們進入一個行業,重要的不是埋頭去努力去堆積一萬小時定律,而是要先擡頭去找那條「等時曲線」,通俗地說,就是不要用戰術的勤奮掩蓋戰略上的懶度,先找到實作目標的最短路徑。
耐心找到這條曲線,不要著急,過程中遇事不要驚慌,因為你知道,要是運氣好,你期待的結果會來得比較早,即使運氣不咋地,你也很篤定結果最終會到來。
既然事情的發展有自己的內在規律,那我們就把自己能掌控的事做好,把不能掌控的事交給規律,交給大數定律。「急、慌」等情緒不僅對於事情的發展沒有幫助,還有可能適得其反,慌亂之中亂動作,走錯步出錯棋。
埃隆馬斯克送到太空中的那輛特斯拉跑車,駕駛室螢幕上就寫著「Don’t Panic(不要驚慌)」。

(四)結語
天地不仁以萬物為芻狗。你有你的情緒,但世界的執行是冷酷的,是由各種冰冷的定律組成的。
人類社會,就是一個大型的白努利試驗場,對於冷面的命運之神,每個個體就是她手裏的那一枚枚硬幣,少部份人會受到命運之神的青睞,他們一出生就在羅馬,但絕大部份人,一出生註定就是騾馬。
但萬幸,現在留給我們這些絕大多數人的,還有「選擇」與「時間」。
但只要有這兩樣,我們就能去探尋人生的概率,人生無常,但我們仍能從中發現一些「有常不變」的東西,英國作家白哲特說:「生活是概率的學校,在這所學校裏,我們每個人不應該甘心當一個被扔來扔去的骰子。」
2023年,樓市有巨大的上漲空間,股市給我們埋下了巨大的上漲希望,職場也是靈活就業的人越來越多,很多人說24年也不要抱有太大期望,我不敢說太多。
在【樂隊的夏天】的第一季裏,九連真人的一首歌讓我印象深刻——【莫欺少年窮】,為何莫欺少年窮?
因為少年們最大的優勢,就是擁有從「頻次收斂到概率」過程所具備的核心因素:
——時間。
(完)





![240221上海]園林工程估算指標(124頁)](http://img.jasve.com/2024-2/60f83e76e70db7cb12e18f75ec19db9d.webp)





