【復分析:視覺化方法】是復分析領域的一部名著,開創了數學領域的視覺化潮流,自首次出版以來,已重印了十多次,深受世界讀者好評。【復分析:視覺化方法】用一種真正不同尋常的、獨具創造性的視角和可以看得見的論證方式解釋初等復分析的理論,公開挑戰當前占統治地位的純符號邏輯推理。作者透過大量的圖示使原本比較抽象的數學概念,變得直觀易懂,讀者在透徹理解理論的同時,還能充分領略數學之美。
該書譯者為武漢大學前校長、著名數學家、教育家齊民友(1930年2月-2021年8月)先生。本書引起了廣泛的關註和討論,齊老師也有些個人思考,於是他以這本書為例,做了深刻的探討,寫下了這篇「譯後記」。

來源 | 【復分析:視覺化方法】
作者 | [美]卓斯坦·尼達姆
譯者 | 齊民友
【復分析:視覺化方法】譯後記
我在轉譯過程中看到幾位讀者對本書的評論, 還有一些刊物上的書評, 以及讀過部份內容的讀者的意見。他們幾乎一致的看法是, 這本書有很高的獨創性:在一門有近200年歷史, 而且已經有了數十部公認名著的基礎分支學科裏, 能夠寫出如此不同凡響的著作, 實在難得。
但是應該承認, 本書仍然是一本基礎教科書。因為一方面它的基本內容確實屬於復分析的傳統領域; 另一方面, 它所要求於讀者的預備知識也僅限於「比較認真地」讀過微積分與線性代數 (當然, 「比較認真地」也是說起來容易做起來難) 。那麽, 還有什麽可以向讀者說一說的呢?

齊民友(1930年2月-2021年8月)
Ⅰ
這本書的書名就標明了視覺化。視覺化當然屬於當前最熱門的時尚「品牌」, 而且完全是由資訊科技衍生出來的。
那麽, 本書的要點是否是教讀者如何使用電腦之類的方法呢?否。本書確實強調電腦的作用, 甚至許多習題需要用電腦來完成。但是, 正如作者指出的那樣, 應該像物理學家對待實驗室那樣對待電腦:用它來發現或驗證新思想, 解決新問題。
作者認為, 他的這本書出生於「牛頓的【原理】一書的創世紀中」。他從牛頓那裏學到了方法, 甚至學到了技巧。這就是強調問題的幾何本質; 或者說, 強調從事物的幾何與物理側面來直觀地理解事物。
著名數學家基利因 (即埃爾朗根綱領的提出者) 在他的名著【高觀點下的初等數學】(此書中譯本由復旦大學出版社出版) 的第1卷關於「數學的現代發展及一般結構」的一節中指出, 數學的發展和教學有三種行程, 即行程A、行程B和行程C。

行程A的特點是強調概念的明確性, 邏輯上的無懈可擊, 方法的單純性, 逐步演繹, 環環相扣, 絕無不必要的引申, 總之, 使數學成為嚴整的體系。其陳述方式是:定義、定理、證明、推論, 等等, 每句話、每個式子都要有根據。
行程B, 這是基利因特別推崇的行程, 強調數學概念的生成和發展, 強調各個分支的相互聯系, 強調邏輯推理背後的直覺和物理內涵。其陳述方式主張夾敘夾議, 娓娓道來, 生動活潑, 發人深省。已故的吳大任教授在為【高觀點下的初等數學】中譯本寫的序言中說, 基利因的思想可以用「融合」二字來概括:數學與物理學的融合, 數學各分支的融合, 邏輯推理與直覺的融合, 還有數學的邏輯展開與歷史發展的融合。
基利因還以歐拉公式
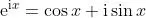
為例詳細比較了行程A和行程B。他尖銳地批評了當時 (指19世紀末) 的德國數學教學。實際上, 他的批評對我們今天的教學也完全適用:這個e是怎樣來的?為何以它為底的對數稱為自然對數?其「自然」何在?歐拉公式難道是天上掉下來的嗎?
我自己就遇到過類似的問題:冪級數
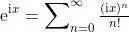
的每一項都沒有周期, 為什麽加起來以後就出現了周期?總之, 學生們在邏輯上接受了某個結論, 不等於「實際上」理解了這個結論。這就是在教學上過分強調行程A帶來的副作用。
本書作者強調自己是認真研究了牛頓的【原理】以後才理解的, 必須從數學問題的直覺、經驗的側面去「體會」數學, 才能得到真正的理解, 才能「悟」其真諦。因此, 他用了極大的精力去探求復分析的許多我們已經非常熟悉的結論的幾何內涵和處理方法, 包括對上述歐拉公式的理解。所以, 讀後確有耳目一新之感。
比較基利因的說法與作者的說法, 這本書可以說是作者在按照行程B幫助讀者教或學復分析上所做的努力, 而作者取得的成功是有目共睹的。
行程C是另外一回事, 這裏不去討論。
如果要比較行程A和行程B的優劣, 就會得到行程B遠優於行程A的結論。本書作者當然是這樣看的。但是, 基利因盡管充分評價行程B, 而且一直身體力行, 但沒有說出孰高孰低。他認為, 這兩種行程都為數學發展所必需, 互相切磋, 又互相補充。基利因說得很對, 在教學與研究中, 采取哪一種行程, 視各人的學識素養與愛好而定, 也視整個數學發展的需要而定。
為什麽牛頓特別傾向幾何學?至少部份由於在牛頓的時代幾何學最為成熟, 而且是人們 (不只是牛頓) 解決科學問題的最有力工具。牛頓以及他同時代的大科學家(還應加上伽利略) 都是歐氏幾何的高手。他的【原理】一書可以說是充滿了求解「幾何難題」的例子, 以致微積分的基本思想——略去高階無窮小, 也時常隱藏在幾何難題後面, 所以讀起來很難得其三昧。說個笑話:如果你不能放開慧眼, 從幾何與物理角度審視問題, 就難以看穿大千世界; 但是, 如果你這樣做了, 立定足跟, 循此漸進, 自然能進入牛頓的不二法門——一種幾何化的物理科學。
本書作者這樣的做法, 值得我們效仿。這當然有很大的難度。所以牛頓以後, 如歐拉、拉格朗日和拉普拉斯, 就以分析的方法來處理同樣的問題。歐拉說過, 完全幾何的方法, 時常難以解決力學問題, 或者只能部份地解決; 而拉普拉斯的名著【天體力學】則把天體運動的研究完全歸結為研究微分方程式。再考慮到微積分的基礎經過兩百多年的錘煉, 借助
語言得到了較完美的解決, 行程A就占據了統治地位。當然, 從幾何和物理側面考察問題的方法, 也就退居後台了。
19世紀的數學發展, 風向似乎又有了改變。這裏起了決定作用的有高斯, 特別是黎曼 (他是本書特別推崇的大師) 。「回到牛頓」可能是20世紀才有的口號, 但是潮流的改變在當時已經十分明顯。不妨說, 這是本書的一條主線。但是, 作者並沒有簡單地著力於幾個幾何難題(但是看來本書作者對幾何難題情有獨鐘, 所以本書中有不少很有趣的幾何題) , 所謂強調幾何和物理實質, 其具體內容讀者能在書中看到。這裏需要特別強調的是, 電腦的出現不僅對於研究工作的影響已經有目共睹, 而且它為數學教學開辟了多麽廣闊的前景遠非我們今天敢於估計的。作者將視覺化展現在本書書名中, 不但是由於數學的本質就有視覺化這一側面, 而且由於今天的資訊科技的現狀使我們能夠在前人無法想象的程度上揭示這個側面。
當然, 任何事物都有兩個方面。強調了幾何直覺一面, 就有可能對於數學嚴格性有所忽視。作者並沒有回避這一點。他明確地宣稱, 他總是把「洞察力」置於嚴格性之前。為了得到更深刻的洞察, 寧可 (在某種程度上) 犧牲嚴格性。全書基本上沒有用
語言, 而且非常自由地把小量與無窮小量混起來用。作者常用「最終相等」之類的說法, 時常把相差高階無窮小就說成是相等。
當然, 作者明白地說, 這些說法都有確切的數學含義, 但是他並不引述任何一本數學書, 而是引證了一位大物理學家S. Chandrasekhar的 Newton's Principia for the Common Readers 一書 (在這部關於復分析的近600頁的大書裏, 竟然沒有魏爾斯特拉斯的名字, 這恐怕只能以作者是「性情中人」來解釋了) 。
讀者當然會問, 這樣做利弊如何, 是有利於學生更深刻地理解數學概念、方法、理論的實質, 還是實際上在鼓勵一種大而化之的空疏作風?這當然要看教學的實際情況而定。但是, 問題並不如此簡單。例如在第5章裏, 作者實際上宣布了, 一個解析函數序列只要收斂, 必可逐項求導。這當然是錯了, 但是, 即使像柯西這樣的大師, 也犯過類似錯誤。正是阿貝爾以致魏爾斯特拉斯等人按照行程A的要求正確地處理了這個問題, 否則就不會有今天的復分析。
至於譯者, 在大多數問題上是尊重了原作者的處理, 但在這類問題上, 就不能簡單、客氣地說原書錯了, 只好寫一個比較長的註腳。這裏並不是討論數學方法論或教學論的合適地方, 但是應該指出, 並非所有數學概念、方法和理論都可以或者適合於視覺化。行程B和行程A相輔相成甚至相反相成, 能不能說, 行程B幫助我們放開慧眼, 而行程A則讓我們立定足跟?對於譯者, 本書的啟示在於, 數學書沒有一個至高無上不得違抗的寫法, 現今最流行的不一定是最好的, 更不一定是最適合你的。這就給學數學和教數學留下了廣闊的創造空間。
Ⅱ
一個數學分支被認為是基本分支, 一門課程被認為是基礎課, 有兩個原因:首先它從其他分支吸取營養; 其次它又影響其他分支的發展或其他課程的教學。數學和其他極為廣博的科學一樣,雖然是一座高聳入雲的偉大建築, 必然有一些最為基礎、影響又最為深遠的思想和方法等, 這些可以說是其精華。基礎課的教學有一個無可推卸的責任, 就是把這些精華交給學生。
為此, 按當前流行的做法, 就是開許多課程, 各司其職, 分兵把關。姑且不論多數學校有沒有可能開這麽多課程, 即使開設了, 也一定會助長各門課程孤立分離, 看不到數學作為一個整體是如何在發展, 有什麽真正關鍵的問題。這也是行程A帶來的副作用。因此, 解決之道, 在於從行程B找出路。
正如吳大任先生給基利因的思想所做的概括:在融合二字上下功夫。下面看一下本書是怎樣處理這個問題的。作者按照復分析發展的內在要求, 也按照自己的科學興趣, 選擇了三個問題, 使讀者能從數學發展的整體來看待復分析, 引導讀者走向更廣闊的科學天地。
A. 幾何學和非歐幾何
什麽是幾何學?基利因在他的【埃爾朗根綱領】裏給出了回答:幾何學所研究的就是幾何圖形在某類運動所成的群下面的不變性質。這本是每一個想學數學的大學生都應該了解的。遺憾的是, 絕大多數大學生也就只是知道這一句話而已。似乎多數大學裏也找不到一門課認真地解釋這個極其重要的思想 (但是有不少大學為文科學生開設的「數學與文化」之類的課程裏卻簡單地介紹了一下) 。
原因可能在於, 現在中國多數大學數學系裏, 幾何教學很不恰當地被削弱了, 而一門幾何課要能夠認真地介紹【埃爾朗根綱領】, 必定有相當份量, 對教學兩方面都是不輕的負擔。

作者還指出, 物理學中有許多類似情況是復數的用武之地。例如 (下面的例子是譯者在教學中遇到過的, 而不一定就是作者心目中所想的, 因為作者的興趣明顯地在於理論物理等方面) 我們在工科數學中都會講如何用復數講交變電流和振動現象, 表面上看, 這也是一種「方便」, 其實, 稍想一下就會發現, 並不是電流、電壓等取了虛數值, 而是實數現在已經不足以描述它們。需要平面向量, 而平面向量就是復數。這裏的情況和二維歐氏平面的運動需用復數來描述是一樣的。
讀者自然會問, 是否有一種「空間復數」足以描述三維歐氏空間的運動?從作者的分析看到, 這是不可能的。怪就怪在, 到了四維歐氏空間卻又可能了, 這就是四元數。對大學生講四元數, 「離經叛道」, 匪夷所思。
然而, 作者非常順暢地引導讀者和他一同在這條思想的小道上漫步, 真可謂「花徑不曾緣客掃, 蓬門今始為君開」。關鍵在於, 放開慧眼, 得到了一個深刻的洞察:數學為的是更加深刻地描述大自然。當然, 這樣做要有本事, 具體說來就是要比較認真地讀過線性代數。其實, 所用的線性代數知識有限, 並無「超綱」之嫌, 很容易懂。問題仍然在於, 大學生們是否想過「線性代數還可以這樣讀」, 那麽很好, 這本書這樣告訴你了, 幫助你放開慧眼。
再轉到非歐幾何。這時我們遇到的情況也與以上說到的相仿, 可能大多數學生知道的僅限於幾何學中的一樁「公案」:過直線外一點對此直線是否可以做出恰好一條 (或多於一條或少於一條) 平行線, 或者三角形三內角之和=(>,<)π。但是, 每一個學數學的學生都應該知道, 在高斯, 特別是黎曼以後, 問題的癥結就變得很明顯了:「現實的物理空間是什麽樣的空間?是否是歐氏空間?」這個問題在黎曼手上成了一個微分幾何問題。於是出現了內蘊幾何與外在幾何的區別和聯系, 出現了空間的度量問題、曲率問題, 等等。
貝爾特拉米發現曲率為-1的常負曲率曲面——偽球面上的幾何就是雙曲幾何, 即羅巴切夫斯基的非歐幾何, 他還做出了幾個不同的偽球面映為平面的對映 (本書就說是幾種不同的地圖) , 得到了羅巴切夫斯基的非歐幾何的幾種不同的「模型」。那麽, 非歐幾何也是幾何, 按照基利因的觀點應該有相應的運動群。而龐加萊發現這些運動全是默比烏斯變換
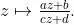
於是非歐幾何與復分析的深刻內在聯系浮出了水面。在講復分析的同時也講非歐幾何就是題中之義了。
在20世紀50年代曾出版過一本從蘇聯引進的教材:普裏瓦洛夫的【復變函數引論】, 認真來說, 它只是用小字號文字介紹了默比烏斯變換, 並且兼及羅巴切夫斯基度量。後來大概再也沒有哪本教材涉足於此。於是學生們對非歐幾何的了解, 最多也就是當作一樁公案, 或者只知道一點公理系統的相容性獨立性。對於它在現時數學發展中的地位作用就不明白了。
總之, 我們失去了一個讓學生接觸一項數學精華的機會。本書可以說是「借題發揮」, 簡單而負責地介紹了有關知識, 使得大學生在低年級就能不太困難地接觸內蘊幾何的許多基本思想, 直到高斯的絕妙定理 (Theorema Egregium) , 而且告訴學生們, 如果想在這條微分幾何的路上走下去, 你可以讀些什麽。作者認為這是復分析的意義最為重大的一部份, 這當然是由於他是潘洛斯的學生, 走的是潘洛斯的路子。在此願請讀者去找一下華羅庚先生的【從單位圓談起】一書。華先生也是沿著自己的學術道路(例如多復變函數論和矩陣幾何等) 介紹了許多關於非歐幾何的知識, 讀後必可大獲教益。
B. 拓撲學與復分析
拓撲學與復分析有著深刻的內在聯系, 這已是眾所周知的事情。可以沿著多種不同的途徑來揭示二者的聯系。例如, 把積分回路看成某個同調類的元, 被積式 (一個微碎形式) 看成餘調類的元, 積分是二者的對偶。由此再進一步就到達了de Rham理論。許多書都是這樣做的, 只是走多遠各有不同。

高斯的證明本質上是一個拓撲證明, 而且就是依賴於上述的連續函數的介值定理。但是高斯並未認識到這是一個有待證明的重要定理, 是波爾察諾指出了高斯的毛病。其實波爾察諾是想用我們現在使用的實數完備性的結果來證明, 但他也不知道實數完備性理論一直到19世紀末才完全地確立。那麽, 看起來需要的是在二維平面 (即複數平面) 上建立上述的不動點定理。回到本書, 作者不是簡單地說代數基本定理是復分析的某個具體結果的推論,(是偶然的推論嗎?) 而是進一步看出復分析這麽一大塊都具有拓撲學的本質。

C. 黎曼的思想
1851年, 黎曼發表了以高斯為評閱人的著名博士論文, 題為【單復變函數的一般理論基礎】 (「Grundlagen für eine Allgemeine Theorie der Funktionen einer veränderlichen complexen Grösse」) 。高斯通常很少稱贊他同時代的人, 但是對於黎曼他卻熱情地稱贊說:「黎曼先生送出的這篇論文令人信服地證實了他在這篇論文處理的主題上深刻而徹底的研究, 表現了一種創造的、富有活力的、真正的數學才智, 一種光輝的富有成果的獨創性。」

這並非由於狄利克雷發現了這個方法, 事實上, William Thomson (即凱爾文勛爵, Lord Kelvin, 這是他的貴族封號, 而不是人名, 但是人們時常弄混了) 、Kirchhoff, Stokes和高斯本人都使用了它。黎曼是因為這是狄利克雷教他的, 所以這樣稱呼。黎曼用這個方法證明了共形對映的基本定理。尤其值得註意的是, 黎曼是把復變量的解析函數作為靜電場來處理的, 而由把靜電場看成一種理想流體的流場。所以, 在物理上成立的, 黎曼就認為在數學上也成立。他至少是把這樣的方法看成探索數學真理的手段。這是十分值得註意的, 而本書, 特別是在最後三章裏充分發揮了這一點。
黎曼在這篇博士論文中提出了現在以他的名字命名的幾何物件——黎曼曲面。 現在的教本裏通常要麽根本不提黎曼曲面, 要麽就把它說成是一個奇怪的嶗山道士可以鉆過來鉆過去的虛構的「曲面」——一切都是為了「方便」的權宜之計。這就離黎曼的思想相距太遠了。黎曼曲面是具有深刻幾何 (準確些說, 是拓撲) 內涵的數學物件, 而一個解析函數的本性, 可以說是由它的黎曼曲面決定的。
後來, 由於基利因和龐加萊等人的功績, 直到外爾 (Hermann Weyl) 1913年發表【黎曼曲面概念】( Die Idee der Riemannsche Fläche ) 這部名著, 才明確了黎曼曲面是一個微分流形。由於微分流形的概念, 再加上黎曼提出的許多新的拓撲概念或思想, 因此說黎曼是拓撲學的奠基人之一絕不過分。黎曼的這些貢獻對20世紀(以及21世紀) 的數學發展影響如何深遠, 絕非這裏能夠討論的。我們只能就本書的寫法, 介紹一點情況, 以供本書的讀者參考而已。
如上所述, 不妨認為黎曼的函數論是行程B的代表, 那麽, 另一位大師魏爾斯特拉斯的函數論則可以說是行程A的代表。盡管黎曼和魏爾斯特拉斯互相很熟悉, 他們的研究工作互相借鑒也很多, 可是在函數論的發展方向上, 二人卻是針鋒相對:魏爾斯特拉斯認為研究解析函數必須依托其具體的表示——冪級數。從一個冪級數開始, 做一切可能的解析延拓所得的總體, 魏爾斯特拉斯稱之為一個analytic configuration。他認為如黎曼曲面那樣的東西是「超驗的」, 即人類經驗無法接受與理解的, 也是靠不住的。

有人說這就是「雄鷹不去抓蒼蠅」!有了魏爾斯特拉斯, 似乎就用不著再去跟黎曼較勁了。但是數學家是不會放棄這樣精彩的幾何與物理直覺的。經過好幾十年的努力, 直到1901~1902年才由希爾伯特「挽救」了狄利克雷原理, 由此發展起來的理論對於當代的數學和物理等是極為重要的。不過要掌握它, 必須要有行程A的良好訓練。經過希爾伯特「挽救」的狄利克雷原理也部份地失去了原來數學與物理學融合的風韻。這個「故事」是否能夠說明, 行程A和行程B甚至可以是相反相成的呢?
回到本書。作者感到遺憾地說, 由於篇幅的限制, 他不可能完全地介紹黎曼曲面的理論, 雖然他也很想這樣做。這是很自然的, 因為這個理論確實超出了作為大學生基礎課所能夠容許的程度。但是本書最後三章的風格, 恐怕在其他數學教材 (不止是復分析教材) 是未曾見到過的。作者把復解析函數的概念與理想流體的流場、靜電場以及溫度場完全地融為一體。可能讀者會問, 怎麽能夠要求一個數學的學生或老師知道那麽多物理學呢?
作者說, 盡管你對於電場可能很生疏, 但是絕大多數人對於熱和溫度還是熟悉的。其實就靜電場的理論而言, 本書並未超出高中物理學多少。問題的癥結可能是, 學數學的時候總以為物理學是另一個天地, 是我們管不了的; 學物理的時候又很少想到, 這也是數學的用武之地。總之, 沒有按照基利因的行程B所要求的那樣, 在數學和物理學的融合上花力氣。請看本書, 講的是一個解析函數, 也就如同在講一個流場:它可能是源或者匯生成的, 也可能是一個偶極子或多極子生成的; 洛朗級數講的無非就是把這些東西疊加起來, 正冪部份表示在無窮遠處有源或者匯或者其他什麽, 負冪部份表示有限遠處有這些東西; 在某一個流場內放進例如一個單位圓盤, 或者另一個障礙物R,流場的變化就是由R的外域到單位圓盤的外域的共形對映。這樣的變化當然是存在的, 這就意味著這個共形對映也是存在的。
當然我們還需要一個數學證明, 但是應該理解, 這個證明是對一個物理事實的數學說明, 而這個物理事實也就是對一個數學結論的物理說明。這已經十分引人入勝了, 而且還發現了許多原來以為並無聯系的結果, 從雙曲幾何的視角來看原來是一回事。全書就結束在雙曲幾何的和弦的交響中。
如果要用幾句話來說明這一大段文字的意思, 那就是:學了一門基礎課, 就應該是開啟了通向數學發展的主流的一扇門。可不可以說, 這正是本書最值得註意的特點呢?
特 別 提 示
1. 進入『返樸』微信公眾號底部選單「精品專欄「,可查閱不同主題系列科普文章。
2. 『返樸』提供按月檢索文章功能。關註公眾號,回復四位陣列成的年份+月份,如「1903」,可獲取2019年3月的文章索引,以此類推。
版權說明:歡迎個人轉發,任何形式的媒體或機構未經授權,不得轉載和摘編。轉載授權請在「返樸」微信公眾號行內系後台。











