過直線外一點可做幾條平行線？歐氏、羅氏、黎曼幾何的區別和套用

前言：這次不寫物理，換成數學。數學和物理雖同屬於邏輯思維，但是數學更加抽象，包括筆者在內的多數物理愛好者最怵的的就是數學，尤其是微積分，這大概就是網上「偽民科」一詞的由來。

數學中的幾何包括三大類：歐氏幾何、羅氏幾何、黎曼幾何，其中羅氏幾何和黎曼幾何統稱為非歐幾何。

歐氏幾何就是歐幾裏得幾何，是我們中學階段學習的知識 ， 用我們最熟悉三維空間和四維時空即可表示。

歐幾裏得（公元前330～公元前275），古希臘偉大的數學家

我們首先回憶一下歐氏幾何的五大公理是：

1. 任意兩個點可以透過一條直線連線；

2. 任意線段能無限延伸成一條直線；

3. 給定任意線段，可以以其一個端點作為圓心，該線段作為半徑作一個圓；

4. 所有直角都相等；

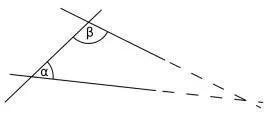
歐氏幾何第五公理

5. 若兩條直線都與第三條直線相交，並且在同一邊的內角之和小於兩個直角，則這兩條直線在這一邊必定相交。

歐幾裏得的【幾何原本】，沿用了兩千年的巨著

這些公理是歐幾裏得在【幾何原本】中提出的，並以此為基礎構建了幾何學體系。【幾何原本】共分為13卷，內容涉及平面幾何和立體幾何的各個方面，包括內容：點、線、面、角度等基本概念和關系；圓的定義、切線、割線、弦、內接和外接等概念及其性質；相似三角形和多邊形的性質；等差數列和等比數列；一次方程式和二次方程式的求解；球、圓柱、圓錐等立體圖形的表面積和體積的求解以及分割……這些知識我們在初中和高中都學習過，內容包羅萬象，此處無法一一詳細介紹。

【幾何原本】作為歷史上最偉大的幾何學著作，一直沿用至今，對我們產生了深遠的影響。後來在此基礎上發展了四種座標系：

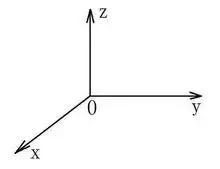
笛卡爾座標系

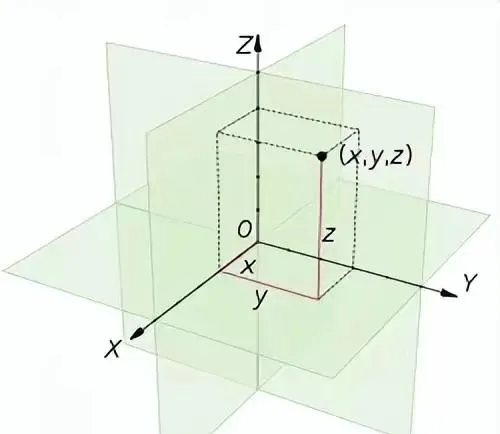
1-直角座標系，即笛卡爾座標系：在同一個平面上互相垂直且有公共原點的兩條數軸構成平面直角座標系，透過X和Y座標值即可確定一個點的位置，也可以用X、Y、Z軸組成空間座標系。

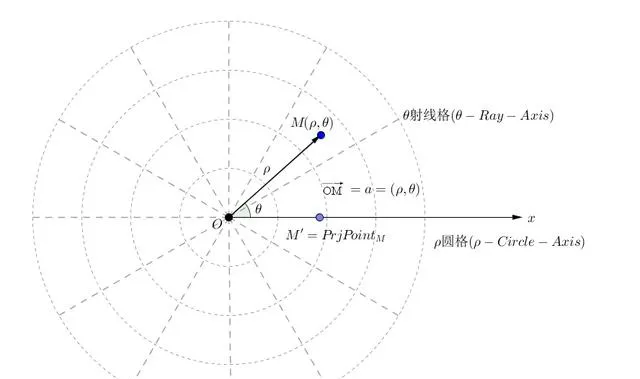
極座標系

2-平面極座標系：極座標，是用於平面中定位點的系統，它以一個固定點O（原點）和一條從原點發出的射線（通常是正x軸）作為參考。座標用（r，θ）表示，其中r是原點到任意點P的距離，θ是線段OP與軸線之間的夾角。笛卡爾座標（x，y）和極座標（r，θ）之間存在一個簡單的關系，即：

x=rcosθ和y=rsinθ。

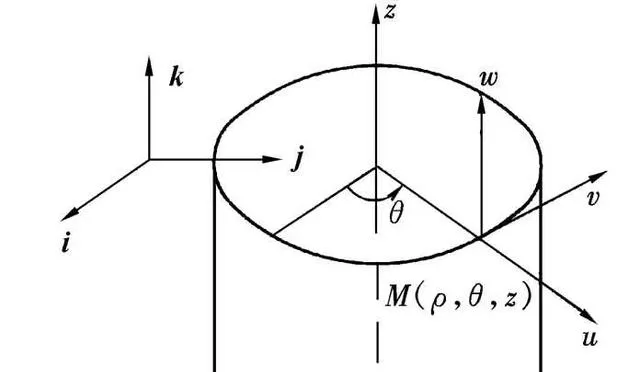
圓柱座標系

3-圓柱座標系：圓柱座標系是一種三維座標系統。它是二維極座標系往 z-軸的延伸。添加的第三個座標專門用來表示 P 點離 xy-平面的高低。徑向距離、方位角、高度，分別標記為ρ，φ，z。

4-球座標系：球面座標系是表示三維空間中某一點的另一種方式。它也要求三個數值，其中兩個是角度，第三個是距離。與笛卡爾座標系換算關系為X=rsinφcosθ，

Y=rsinφsinθ，Z=rcosφ。

希爾伯特（1862～1943），德國數學大師，被稱為數學界的「無冕之王」

從上可以看出，極座標、圓柱座標、球座標都是可以轉化為笛卡爾座標的，多個維度座標可以構成空間。而數學空間可以被擴充套件來套用於任何有限維度，而這種空間叫做n維歐幾列特空間（可以簡稱n維空間）或有限維實內積空間，或稱為希爾伯特空間。

羅巴切夫斯基（1792～1856），俄羅斯數學大師

羅氏幾何就是羅巴切夫斯基幾何，也稱雙曲幾何，是一種獨立於歐氏幾何的公理系統，雙曲面立體圖形類似馬鞍的形狀。

羅氏幾何的空間曲面是雙曲面，像馬鞍形

雙曲面的方程式通常采用下列形式：

Ax² + By² - Cz² = D

其中，A、B、C、D是常數。當A、B、C中至少有兩個正號時，該方程式描述的曲面是一類雙曲面。如果A、B、C中都是正號，稱為雙葉雙曲面；如果A、B、C中只有一個正號，稱為單葉雙曲面；如果A、B、C中全是負號，稱為超雙曲面。雙曲面具有一些獨特的性質，如其具有兩個相互獨立的拱形。

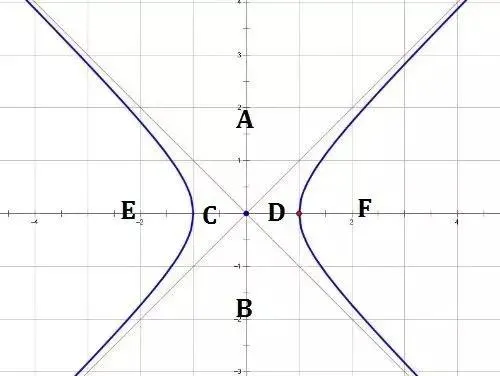
標準雙曲線，兩條漸進直線構成光錐

如果將雙曲面投影到XY平面，則得到我們中學時學過的標準雙曲線：

x²/a² - y²/b²= 1 (a＞0，b＞0)

黎曼（1826～1866），德國偉大的數學家

黎曼幾何是非歐幾何的一種，亦稱「橢圓幾何」，黎曼幾何的模型是一個經過適當「改進」的球面，黎曼空間本質上是彎曲的。

黎曼幾何的空間曲面是橢圓球面

黎曼幾何發展了空間的概念，黎曼提出了n維流形概念，他認為幾何學中的研究物件為「多重廣延量」，空間中的點可以用n個實數（x1, x2, …, xn）作為座標進行表示。黎曼幾何是一種研究曲線、曲面與曲率的幾何學。在黎曼幾何中，最重要的是曲率的計算。曲率是描述曲線、曲面的彎曲程度的量。在二維曲面上，曲率可以透過計算曲線的切向量和法向量之間的夾角來得到。對於一個給定的曲線，其曲率可以透過以下公式計算：

K(s) = |dT/ds| / |ds/ds|

其中，K(s)表示曲線在參數s處的曲率，dT/ds表示曲線的切向量沿s方向的導數，ds/ds表示曲線的弧長在s方向的導數。

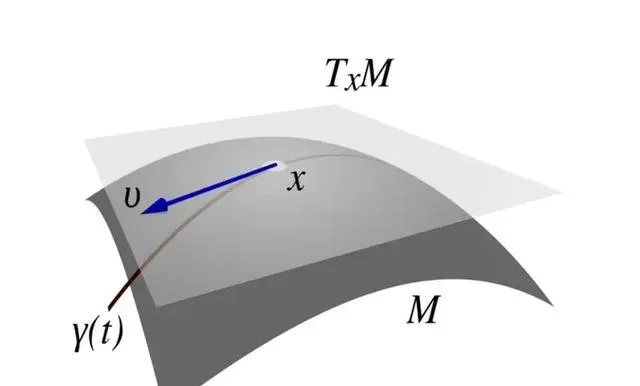
黎曼幾何中點x的曲率向量u和切面TxM

對於三維曲面，曲率的計算可以透過計算曲面上兩個相互垂直的方向上的曲率來得到曲面的曲率。具體而言，曲面的主曲率可以透過以下公式計算：

k1 = (E * G - F^2) / (E + G ± √((E - G)^2 + 4F^2))

k2 = (E * G - F^2) / (E + G ∓ √((E - G)^2 + 4F^2))

其中，E、F、G分別是曲面的第一、第二、第三基本形式的系數。k1和k2分別表示曲面的兩個主曲率。

黎曼度規張量計算公式：

g_μν = ∂x^α/∂x^μ * ∂x^β/∂x^ν * g_αβ

克氏符號計算公式：

Γ_μν^α = (1/2) * g^αβ * ( ∂g_βν/∂x^μ + ∂g_βμ/∂x^ν - ∂g_μν/∂x^β )

黎曼曲率張量計算公式：

R_μνλ^α = ∂Γ_μν^α/∂x^λ - ∂Γ_μλ^α/∂x^ν + Γ_ρν^α * Γ_μλ^ρ - Γ_ρλ^α * Γ_μν^ρ

這些公式用於計算黎曼幾何中的度量張量、克氏符號和曲率張量，以研究曲面的內稟幾何性質和曲率。這些公式是黎曼幾何的基礎，用於描述非歐幾何空間和廣義相對論中的時空彎曲。

歐氏幾何、羅氏幾何、黎曼幾何我們已經做了初步的介紹，下面我們將介紹三種幾何學的區別：

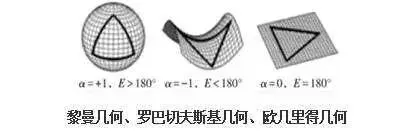
三種幾何的曲率對比

1- 歐氏幾何是曲率恒等於零的平面幾何，羅氏幾何是曲率為負常數的曲面幾何，黎曼幾何是曲率為正常數的曲面幾何。 圖中可以看出以上三種幾何空間分別為平面、凹面、凸面。

黎曼曲率等於1、-1和0的空間分別是黎曼球空間、羅巴切夫斯基空間和歐氏空間，歐氏空間可看作黎曼空間的特例。

2- 過直線外一點，可以做幾條直線與該直線平行？歐氏幾何認為是一條，羅氏幾何認為是至少兩條甚至無數條，黎曼幾何認為是沒有。

歐式幾何第五公設認為，過直線外一點做一條直線，有且只有一條直線與該直線平行，這是我們認知範圍之內的。

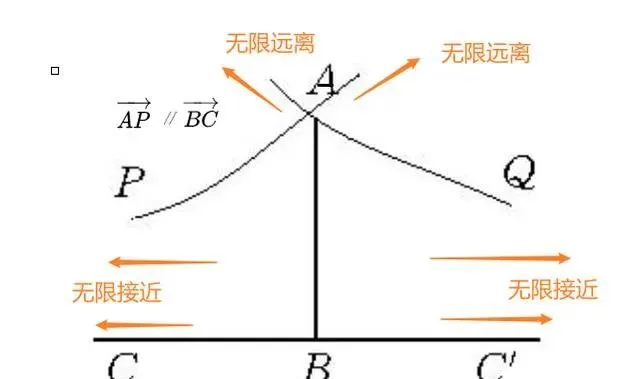
羅氏幾何認為直線外一點，有無數條直線與已知直線平行

羅氏幾何認為可以做無數條直線與已知直線平行，羅氏平面幾何的平行直線和歐氏平面幾何的平行直線的定義是不相同的，在羅氏平面幾何中，所謂已知直線的平行直線，只是與已知直線不相交的所有直線中的特殊直線。在羅氏平面上，若AP∥BC ，則稱直線AP沿 BC方向(或AP 方向)平行於直線BC，記為AP∥BC於方向BC (或AP )。當方向一致時，直線間的平行具有對稱性和傳遞性。在羅氏平面上，過直線CC′外一點A，有且只有兩條直線AP和AQ分別於不同的方向平行於CC′，在羅氏平面上，任何兩對平行線可以互相疊合，且二平行線在平行方向上無限接近，而在反方向無限遠離。

黎曼幾何認為直線外一點做的任何直線，都會與已知直線相交，就是否認平行線存在

黎曼球面幾何平行公理認為，過直線（大圓即「直線」）外一點，沒有平行線。地球上的經線是球面上的直線，而任意兩條經線按照定義都是平行直線，但是這些平行直線都是相交的，它們在南北兩極相交。你在球面上是做不出不相交的平行線的。

三角形內角和：黎曼幾何認為大於180度，歐氏幾何認為等於180度，羅氏幾何認為小於180度

3- 三種幾何的三角形內角和不同。 黎曼幾何歐氏幾何是把認識停留在平面上了，所研究的範圍是絕對的平的問題，認為人生活在一個絕對平的世界裏。因此在平面裏畫出的三角形三條邊都是直的，兩點之間的距離也是直的。

但是假如我們生活的空間是一個雙曲面，我們可以把雙曲面它想象成一口平滑的鍋或太陽罩，我們就在這個雙曲面裏畫三角形，這個三角形的三邊的任何點都絕對不能離開雙曲面，我們將發現這個三角形的三邊無論怎麽畫都不會超出180度，但是當把這個雙曲面漸漸展開時，一直舒展成絕對平的面，這時羅氏三角形就變成了歐氏三角形，也就是我們在初中學的平面幾何，其內角和自然是180度。在平面上，兩點間的最短距離是線段，但是在雙曲面上，兩點間的最短距離則是曲線，因為平面上的最短距離在平面上，那麽曲面上的最短距離也只能在曲面上，而不能跑到曲面外抻直，故這個最短距離只能是曲線。

若我們把雙曲面舒展成平面以後，再繼續朝平面的另一個方向變，則變成了橢圓面或圓面，這個時候，如果我們在這個橢圓面上畫三角形，將發現，無論怎麽畫，這個三角形的內角和都大於180度，兩點間的最短距離依然是曲線，這個幾何就是黎曼幾何。

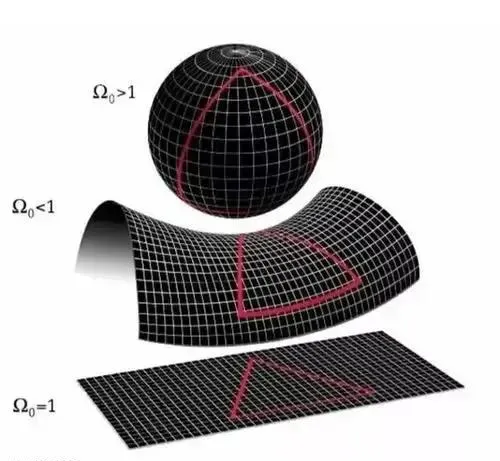
三種幾何求兩點間的距離，圖中一個個無限小的網格代表著微分

4-對於空間上兩點之間的距離定義不同，只有歐氏幾何計算的是最短直線距離。 在歐幾裏得幾何中，曲面上兩個相鄰點之間的距離，由以下形式公式得其距離為ds²=Adx²+Bdxdy+Cdy²

其中A、B和C取決於x和y，可以根據A、B和C本質上確定一點的曲率。

羅氏幾何計算兩點間的距離是雙曲表面上的曲線距離：

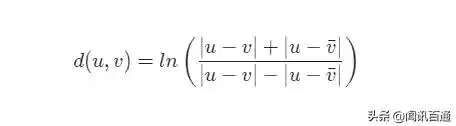
u、v、vˉ是雙曲面空間中的點

黎曼幾何計算兩點間的距離是偽球表面的曲線距離：

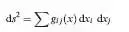
式中系數g ij (x ) 是對稱協變張量場（度規張量）的分量，dx和idxj為曲率二階張量

5- 這三種幾何的數學基礎原理不相同。 黎曼幾何作為非歐幾何的一種, 它與羅氏幾何相比, 有著實質性的不同。羅氏幾何主要工作是建立了一整套區別於歐幾裏得的【幾何原本】的邏輯體系; 而黎曼幾何的核心問題是以微分幾何為基礎, 建立曲線座標系中的微分方法。

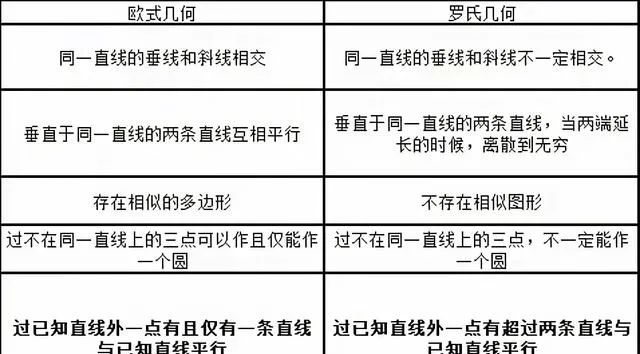
羅氏幾何與歐氏幾何理論上存在根本的差別

羅氏幾何學的公理系統區別於歐式幾何學之處, 僅僅是把歐式幾何平行公理改為: 從直線外一點, 至少可以做兩條直線和這條直線平行。

黎曼幾何與羅氏幾何的平行公理相反: 過直線外一點, 不能做直線和已知直線平行。也就是說, 黎曼幾何規定: 在同一平面內任何兩條直線都有公共點, 黎曼幾何學不承認存在平行線。很自然就有另一條公設: 直線可以無限延長, 但長度是有限的, 這可以類比為一個球面。

黎曼幾何是非歐幾何的一種，亦稱「橢圓幾何」。黎曼幾何的模型是一個經過適當「改進」的球面。黎曼幾何對曲率沒有限制，包括了各種曲率可變的空間。黎曼幾何中給定黎曼度量，就可以討論「測地線」，大意是球形上連線兩點的最短的曲線。

三種幾何中黎曼球體幾何最為復雜，是以微分和張量為基礎建立的

對歐式幾何來說，兩點間直線段最短，因此測地線就是直線。

對球面幾何來說，兩點間的最短曲線是大圓的弧, 因此測地線是大圓（即所在平面過球心的圓）。所以在球面幾何中，緯線並不是「直線」。任意兩個大圓都會相交於一對對徑點，因此不存在平行線。球面幾何其實不成立「兩點決定一條直線」的定理，所以球面幾何其實並不是橢圓幾何，不過在進行某種技術處理之後可以使其成立。黎曼幾何中的測地線的每個「小段」都是連線兩點的最短線。可以參考歐式幾何（其實也是黎曼幾何的特例）中的直線。當然直線不僅「小段」是最短的， 而且是其上任意兩點間的最短線。在球面幾何中， 大圓的劣弧是最短線，優弧不是， 所以要加上「小段」的限制。

6- 三種幾何在套用科學中的套用範圍是不同的 。

歐氏幾何適應範圍最為廣泛，我們也最為熟悉

在我們這個不大不小、不遠不近的空間裏，也就是在我們的日常生活中，歐式幾何是適用的。比如牛頓經典力學三大公式、薛定諤方程式、麥克斯韋方程式組、狹義相對論、弦理論等，都是用歐式幾何空間來建立數學模型的，這也是我們最常用和最熟悉的。

羅氏幾何可以用於描述宇宙中的量子世界

量子力學中，羅巴切夫斯基的雙曲幾何學模型可以用於描述粒子在雙曲線空間中的運動。具體來說，量子力學中的自旋空間可以被看作是一個雙曲線空間，而波函數則是這個空間中的向量。根據羅巴切夫斯基的模型，這個自旋空間可以被看作是一個雙曲線空間。在宇宙空間中或原子核世界，羅氏幾何更符合客觀實際，比如量子力學的迪拉克方程式、量子電動力學、量子統一場論等，都是以羅氏幾何來建立數學模型的。除此之外，機器人學、圖形設計、芯片制造等行業也要用到羅氏幾何。

在地球表面研究航海、航空航天、宇宙研究等實際問題中，黎曼幾何更準確一些。黎曼幾何在物理上非常有用，因為光在空間上就是沿著曲線跑的，並非是直線，我們生活在地球上，因此我們的空間也是曲面，而不是平面，但為了生活方便，都不做嚴格規定，都近似地當成了平面。

黎曼統一了黎氏幾何，羅氏幾何，歐氏幾何，並且預見物質的存在可能造成空間的彎曲，為愛因斯坦的廣義相對論準備了數學基礎。廣義相對論認為，地球並不是受重力牽引而保持慣性運動，而是由於太陽的質素使空間彎曲，地球的彎曲軌域根本就是慣性運動軌域，是彎曲時空中的短程線（相當於平直時空的直線），彎曲的空間就是把最短線定義為直線。那麽我們可以說，廣義相對論、黑洞理論、蟲洞理論、宇宙大爆炸理論等，都是以黎曼幾何來建立數學模型的。

以上就是歐式、羅氏、黎曼幾何的全部區別。簡單的說就是，歐式幾何表示的是平直時空，羅氏幾何和黎曼幾何表示的是曲面即彎曲的時空（有的文獻稱之為流體面），歐氏幾何是羅氏幾何和黎曼幾何的特定條件下的近似空間。歐式幾何可用於我們身邊的宏觀事物及運動，羅氏幾何多用於微觀量子世界，黎曼幾何多用於宇宙中的大質素天體。

至於高斯座標系和閔考斯基座標系，可以分別認為是黎曼幾何和歐氏幾何的延伸和過渡理論，本文將不再單獨將其列出。說句題外話，本文只列舉了六位數學家，居然有四位是德國人，我們不得不承認，德意誌民族是一個優秀的民族 。

本文是數學文章，之所以以其物理套用的內容來結尾，原因很簡單，數學作為一種最重要的工具，是來為其它自然學科服務的，沒有實際套用意義的數學理論是不完美的，或者說是沒有意義的。

後記：我有時在想一個問題，數學和物理是相通的，那麽它們是否和藝術也是相通的呢？老愛在相對論中描述天體彎曲了時空，梵高在作品中用畫筆扭曲了星空，雖然一個是論述宇宙自然，一個是表達人的內心世界，但是二者可能是相通的。心有多大，宇宙即有多大？還是宇宙本來就在我們的心中？