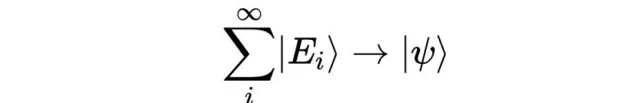如同春风拂面,这正是量子力学为何必须运用「希尔伯特空间」的根本原因。在前文中,我们探讨了量子力学中的向量空间并介绍了态矢量:粒子的量子状态可通过向量空间的态矢量来表达。任何物理量的量子态能够被视作该物理量所有可能结果态的线性组合,并且这些结果态的列表可能是无限的。

此时我有一个简单却至关重要的问题要问:那个量子态的向量空间,它的维度到底是多少呢?这里要特别注意,向量空间的维度实际上是构成基的向量的数量。既然如此,那么在这个向量空间中,基到底包含多少向量呢?量子态或许可以是无数结果态的线性组合。尽管目前还没有证明这些结果侧的列表构成了一个基,但我们可以暂且假定这点(后续的文章中会进一步验证)。这就意味着,基可能会包含无限多个向量,因此向量空间的维度也可能是无穷大!
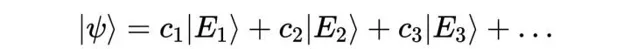
听起来似乎有点不可思议,然而我们确实需要一个无限维度的概念,来用线性代数表述粒子状况。理论上,这一切似乎都很合理,然而当「无穷」这一概念被引入时,确实需要谨慎行事。为了阐明在线性代数中引入「无穷」可能导致的问题,接下来让我们考察一个具体的向量空间示例:实数上多项式构成的向量空间。只有当一组对象满足某些特定规则时,它们才能算作向量空间,这一点很容易验证。

多项式自然地组成一个向量空间,我们可以选取x的所有幂次作为基,从零次幂开始。借助这个基,任何多项式都能被表示为这些基元素的线性组合。现在,若我们将这些线性组合扩展到无穷,会发生什么呢?我们利用基构建一个带有精心选定系数的无穷线性组合。左边是这个线性组合的表达式,右边是其图像。随着项数的不断增加,你可能会察觉到这个函数的样子越来越熟悉,如果项数无穷,那么它便成了e^x的泰勒级数!

这简直让人感到惊奇,毕竟e^x并不是一个多项式,如此一来,我们竟然得到了一个完全超越向量空间的东西!想一想,这就像收集无数石头,不断叠加,最后竟然莫名其妙地变成了一块披萨,天南海北的联想!那么,这究竟是什么问题呢?我认为值得深入探讨,因为引入无穷的方式其实颇具微妙。在这里,答案就在于「无穷」是一个概念,而并非具体的数值。对于任何有限的线性组合,是可以得到一个多项式的,因此属于向量,无论这个组合有多庞大。然而,一旦项数趋近于无穷,极限结果就不再是一个多项式,这样便超出我们的向量空间。

我喜欢用一个图来解析这个问题,图确实展示了我们向量空间所涵盖的区域和边界。线性组合的第一项给出的则是向量空间中的某个元素,随着我们不断添加更多项,线性组合逐渐推进到向量空间的边界。而在无穷项的极限中,结果几乎就处于向量空间的边缘,接近外界。明白为何在向量空间中引入「无穷」是件风险性的事,的确非常重要。那么,对量子向量空间意味什么呢?
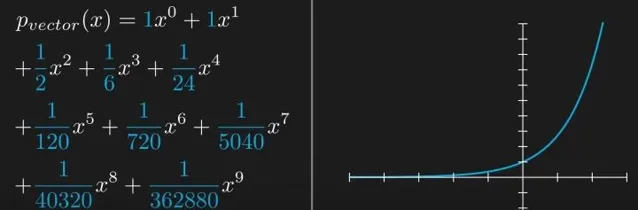
这意味着如果量子态处于结果态的无穷叠加之中,有可能这个量子态会超出向量空间,从而不再属于量子态,这实在是个大麻烦!那么,我们应当如何解决这个问题呢?这显然是一个数学难题,我们可以在量子向量空间里额外定义一个规则,以保证每个收敛的向量和都必须收敛到向量空间中的一个元素,这听上去也许有些搞笑,但这确实是我们的权利。

你或许不敢相信,但我所描述的,实际上便是希尔伯特空间的真谛!希尔伯特空间的定义为具有内积并且完备的向量空间。接下来,我们来逐步剖析这些数学术语:内积其实是广义的点积,具体内容会在后面的文章中介绍。完备性则意味着每个收敛的向量序列(像是无穷线性组合的部分和)都会收敛到向量空间内的某个元素。因此,希尔伯特空间就是一个内积下的向量空间,其中每个收敛的和或序列都能收敛到这个空间的某个元素——这几乎与我们刚才添加的条件是等同的!

如果你希望对完备性有直观理解,我们可以参考向量空间的图示。在多项式向量空间中,我们把无穷线性组合视为位于空间边缘的某点,希尔伯特空间则包罗这些边缘,确保没有任何空隙能让无穷线性组合逃出空间。因此,在这个意义下,它是「完备」的,包含着所有可能的情况。尽管这个图在数学上不够严谨,但我认为它提供了良好的直观理解。所以,希望你能意识到,在量子力学中运用希尔伯特空间是极为合理的;这只不过是我们使用无限维向量空间的一种方式,同时确保在将无穷多个态矢量叠加时,绝不会得到荒谬的结果。我们的目标是,在进行线性组合的过程中,同样能保持量子态的清晰,而不是收获一块不知道从哪里来的披萨。从今天起,我们将把量子向量空间看作希尔伯特空间,通常使用这个符号来表示:所有的量子态都存在于此范围之内。