
粒子可以用向量空间中的向量表示,某种程度上是所有可能测量结果的叠加。物理量(如能量、位置等)则由该空间中的线性算符表示。
既然要使用线性代数的框架,我们应该确保对 什么是向量空间 有扎实的理解。让我们看一下向量空间的数学定义。正式地,向量空间是一个满足以下规则的对象集(称为向量):
对于任何向量 u,v,w 和标量a,b:
大多数规则只是规范我们已经直观理解的概念。比如,第一个规则仅仅说明,两个向量相加得到另一个向量。下一个规则指出,向量乘以标量也会得到另一个向量。而其余的很多规则只是加强了我们对向量如何相加和如何与标量相乘的直观认识。
那么以这种方式定义向量空间的好处是什么呢?这种定义没有提到数字列或箭头。
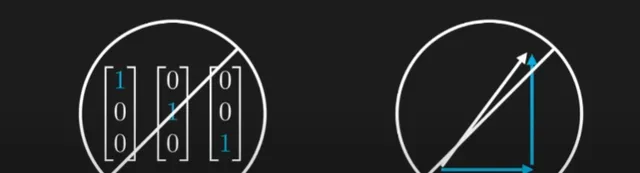
任何满足这些规则的对象集,都可以形成一个向量空间。只要规则正确,它可以是水果,可以是函数,当然也可以是我们熟悉的数字列和箭头。 希望你开始明白线性代数和向量空间更多是关于 结构和模式 ,而不是关于你使用的对象类型 ——恰好向量空间的这种结构正是我们描述量子世界所需的。
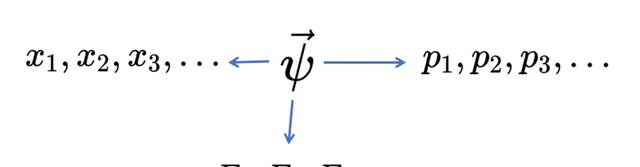
既然我们理解了什么是向量空间,让我们将其应用到量子力学中。我们希望用向量空间中的向量来表示粒子。
更具体地说,向量空间中的向量代表一个 量子态(quantum state) 。 量子态是一个数学对象,它包含了粒子的所有物理属性。 从中我们应该能够提取出在特定时间下可能的位置、动量、能量等以及所有相关的 概率 。
在量子力学中,物理学家喜欢用不同的符号来表示向量。我将使用这个符号来表示向量:
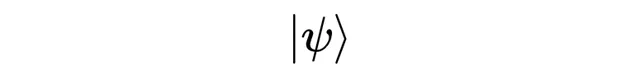
当以这种方式写一个向量时,我们称它为「ket」。它仍然是一个向量,只是符号不同。选择这个符号的原因可能看起来奇怪,但它的威力将在后续文章中显现。
现在让我们将这个符号与量子力学联系起来。前面一篇文章中,我们想用所有可能测量结果的线性组合来表示粒子,例如能量。因此,会有一个代表每个可能能量结果的量子态「ket」的列表,当前的量子态由这些量子态的线性组合(通常称为叠加)表示,
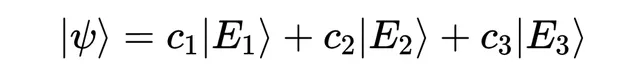
而系数与该结果的概率有关。如果我们想测量角动量,就会有一个代表每个可能角动量结果的量子态「ket」列表,并且会有一个不同的线性组合,
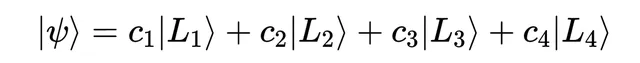
但当前的量子态仍然相同。对于可以进行的每一个测量,情况都是如此。
现在我们有一个有限的结果态列表,但很有可能有无限多的结果。
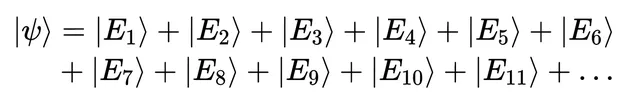
想一想,有什么能阻止你给粒子越来越多的能量呢?我们需要为任意高的能量准备能量结果态。因此,有时我们可能会有无限多个「ket」的线性组合,代表无限多结果的叠加。 后面,我们将简要讨论这种无限带来的一些问题(以及为何希尔伯特空间可以解决这些问题) ,但现在我们假设无限线性组合不会引发任何问题。
然而,有另一个问题需要解决。到目前为止,我们讨论的是当像能量和角动量这样的物理量有离散的一组可能值时的情况。但物理量并不总是离散的!例如,位置。目前,没有实验证据表明位置是离散的 ;电子可以出现在任何地方——没有「列表」可以表示所有可能的位置。 换句话说,位置是连续的(continuous),而非离散的。我们希望能够在理论中以数学方式描述这一点。
所以这里有一个难题:假设电子可以拥有任意可能的位置(尽管有些位置可能比其他位置更可能)——我们如何使用可能位置的「ket」来表示电子的量子态?典型的求和不够用了,因为进行求和需要一个 离散的 列表,而要覆盖所有可能位置是不可能的,即使列表是无限的。
因此,我们需要一种能够对连续集进行求和的数学运算。你可能已经意识到,积分正是这样一个运算。
所以让我们利用积分,在可能结果是连续集合时构造线性组合。首先,我们想将其写成一个和,因此写下积分符号来表示一个和,
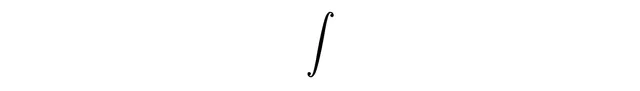
其中上下限默认为正无穷大和负无穷大。接下来,在所有可能的位置结果上求和,用变量x表示,因此需要一个微分dx来表示这一点(不用担心dx放在哪里,在许多理论物理文献中你会看到它放在前面)。
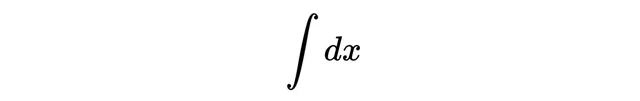
接着,我们需要「ket」,将它们按它们所代表的位置x来标记。
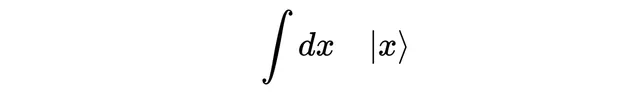
最后,我们需要系数。对于每个可能的位置x,都有一个系数,这意味着需要一个对应于每个x值的数,这正是函数的作用,所以我们使用一个函数来作为系数。
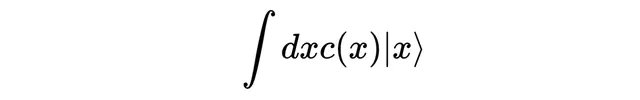
这样就完成了!我们写出了一个量子态,其中叠加的是一组连续的结果。
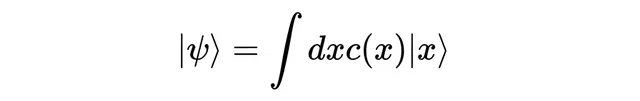
如果你第一次看到这,可能会感到非常困惑。只要记住积分代表一个连续求和,因此这只不过是一个连续的结果态「ket」的线性组合。
继续之前,我想花一点时间讨论这里的「系数函数」。用函数代替系数可能看起来很奇怪,所以让我们看看它是如何形成的。假设位置确实是离散的。在这种情况下,将有一组可能的位置结果及其相关系数。
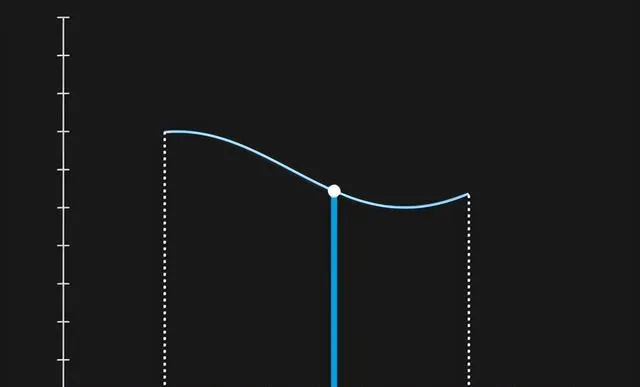
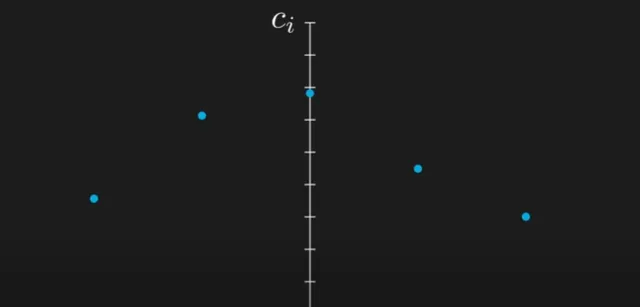
让我们将这些系数作为它们对应的位置的函数进行绘制。对于每个离散位置x,将它的系数c作为一个点绘制出来。
现在,让我们「解除」位置的离散性。让可能位置之间的间隙缩小,填补所有缺失的位置系数。随着这一过程发生,系数开始变得越来越接近,
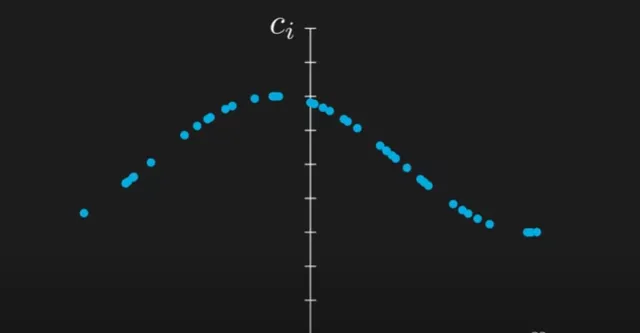
你会看到它们最终形成一条线——换句话说,它们开始形成一个函数!只是假设这个函数必须是连续的 ,但我们将在以后的文章中证明这一假设。这就是我们是如何从离散系数过渡到函数的?
让我们继续并注意到一个重要的事情。记住,在可能结果的线性组合中,系数与获得该特定结果的概率有某种关联。 这意味着这里的函数某种程度上告诉我们关于某个位置的概率。 如果你有一些量子知识,也许你知道有一个与位置概率相关的函数——波函数!事实上,这里的函数就是波函数。
所以,希望你看到在线性代数框架中,位置波函数只是每个可能位置「ket」前面的系数列表。当我第一次学习量子力学时,我一直在想函数如何与线性代数框架联系起来,现在希望你能明白了。很多人常说波函数是一个向量;尽管函数可以存在于它们自己的向量空间中(你可以以这种方式构建量子力学),但现在你知道波函数实际上代表什么了。 在量子力学中,波函数表示每个连续「ket」列表前面的系数。
那么这些系数与波有什么关系呢?为了解释这个问题,我们必须推导出薛定谔方程,但这是后话了。
总结一下:在这个模型中,粒子用向量空间中的向量表示,也称为量子态。我们为这个向量选择了一种特殊的符号,称为「ket」。这个「ket」包含了粒子所有的信息。对于任何物理量,量子态都是所有可能结果「ket」的线性组合(即叠加),系数告诉我们该结果的概率。如果物理量有一组连续的结果,我们用积分代替求和,用称为波函数的函数代替系数。











