女士们,先生们,老少爷们儿们!在下张大少。
图形、数学和非洲
图论是数学的标准组成部分。一个经典的例子是寻找一个推销员访问美国50个州的所有首府一次所需的最短路径。这个所谓的「旅行推销员」问题至今仍是一个未解之谜,尽管已经有了几个「好」的解决方案。两个城市之间的「路径」可以用直线表示,如果方向也很重要,还可以加上箭头。线的形式可以是直线,也可以是粗略画出的曲线,但这并不重要。图论的应用有时是运筹学课程的一部分,从经济学到计算机科学,图论的应用不胜枚举。
大多数运筹学教科书的入门例子都提到了欧拉的七桥问题,即如何走过前德国城市哥尼斯堡的七座桥。如今,哥尼斯堡已成为俄罗斯的加里宁格勒市,七座桥也已不复存在,但在七座桥还存在的时候,欧拉就已经证明,如果同一条路径不能走两次,就不可能走过七座桥。
一个重要的数学特点是,可以利用这些图形进行计算,让数学家获得直观无法发现的惊人结果。例如,对欧拉图进行数学研究时,可将左边的三个点从上到下编号为 1、2、3,并为右边的点加上数字4。在一个称为矩阵的列表中,1表示从该行前面提到的点到该列上面提到的点之间有一条路径。如果没有路径,则使用0。在给出的示例中,主对角线上有0,因为点本身没有循环(图4.1)。

图4.1:沙地版欧拉问题(左)及其数学版(右)
图论的数学力量并非源于欧拉走桥的趣闻轶事或其他有趣的素描,而是源于使用这些「矩阵」的数学技术,从而可以得出结论,而这些结论在纠结的线条中是无法预测的。这一数学版本的优势体现在它的许多应用中,例如四色定理(四种颜色足以为任何地图着色,使得没有两个相邻的国家是相同的颜色)。
非洲的例子也可以作为图论的入门。世界各地的不同文化都会用手指或树枝在沙地上作画,或抬手或不抬手,充满曲折的线条增强了其神话色彩。有时还会加上一些符号,以明确绘画的目的。这表明,不仅舞蹈、音乐或戏剧表现是仪式的灵感来源,数学方案也是如此。
关于非洲图形的故事
来自刚果和安哥拉边境地区的绍奎人称他们的沙画为 「sona」。在村子中心举行的集会上,他们会朗诵这些图画上的故事。在长达6-8个月的启蒙仪式中,每一代人都要学习这些传统图示以及相应的谚语、背诵内容或谜语。
有时使用这些图画的另一个场合是哀悼仪式。据说一个村长死了,有三个候选人来继承他的职位。一幅几何图画代表了这种情况:中间一个大白点代表死去的酋长,另外三个小黑点,分别编号为1、2和3。一条封闭的曲线环绕着三位王位继承人和死去的首领。其中两个候选人在不越线的情况下无法到达死去的酋长身边,但中间的那个候选人可以,因此他成为了新的酋长。在另一幅图中,一条单线将新生儿和逝者连接起来,太阳和月亮在每个凡人的生命中都起着作用,于是也被添加进来(图 4.2)。

图4.2:解释谁成为新首领的图(左)和「生命图」(右)
沙画、记忆辅助工具和绘画图案
一种常用的画图技术是从放置几个点开始,然后移动,就好像一条曲线围绕着这些点编织一样。矩形「框架」的内边缘被认为是镜子,曲线在那里反弹,就好像是一束光线。接下来,在图中放置一些额外的镜子,以生成所需的曲线(图4.3)。

图4.3:五行六点和两面「镜子」(左),由一束假想的光线穿过,而方格则依次被染成黑色、白色、黑色、白色等等(中间),以产生最终的图案,让人联想到非洲织物
围绕这些点构建了一个矩形网络,使这些点位于网络线的交叉点上。在我们的插图中,如果从左下方以45°角插入一束光线,从矩形框下边框的第一个细分点开始,这束光线将描述一条假想的路线,在右上角以极小的路径反弹到右边,然后贴着右边框返回到左下角,以此类推。
当假想光线穿过网络时,一个方格会被染成黑色,然后是白色,接着又是黑色,依此类推,直到整个网络都被染上颜色。最后,就形成了一个几乎无法辨认出原始曲线的图案。这让人想起非洲的织物。
可以用不同的方法排列假想镜面,或者使用更多或更少的点,结果也会不同。在图论中,获得正方形图案的程序(此处使用黑白方框)有时会颠倒过来。例如,在对国际棋盘上的走子进行数学研究时,就采用了这种方法。
非洲绘图专家熟练而毫不犹豫地绘制了这些图形。这里的坐标系是一种记忆法,将记忆任务简化为几个数字和一种几何算法(图 4.4)。

图4.4:来自其他初始条件的其他曲线
沙画推理
玛西娅·阿舍尔(Marcia Ascher, 1988, 1994)是最早关注这些沙画及其与图论关系的人之一。她列出了来自不同大陆的类似图画的清单,并根据地区或人物对图画进行了分类。她还注意到一些数学性质的特性,如图形的倍增(图 4.5)。

图4.5:倍增图形
米乌博人用一些点表示祖先,用其他点表示村庄的小屋。周围的线表示祖先的灵魂影响着部族的生活。当居民人数增加时,图画就必须进行调整,这就是所谓的 「 倍增」图。在其他例子中,图形甚至可以有三重 倍增。
阿舍尔探索的另一个受数学启发的特性是图画中的对称性,如左右、双重左右或旋转对称。许多例子表明,对图画进行不同的分组,例如按照所用点的数量进行分组,可能会很有趣。然而,结构并不总是那么合乎逻辑、简单明了。非洲人的创造力再次展示了令人惊讶的替代方案(图4.6 和4.7)。

图4.6:按照点的数量排列的图画。省略或增加一个点可以得到括号中的类似情况

图4.7:完全不同的对称绘图方法
沙画中的更多数学
当哲学家路德维希·维特根斯坦(Ludwig Wittgenstein)试图为数学的本质下定义时,他指出了图论,并断言 「每个人都会立即认识到它的数学特性」。与阿舍尔几乎同时开始从事民族数学研究的保卢斯·格迪斯(Paulus Gerdes)试图为这些非洲曲线提出一些真正的数学定理(Gerdes, 2002)。
与欧拉桥的第一个例子相比,格德斯采用了不同的矩阵方法。受之前推导出的颜色模式的启发,0 现在对应于正方形的一种给定颜色,1 对应于另一种颜色,如果需要第三种颜色,则对应于 2,以此类推(图 4.8 和 4.9)。

图4.8:作者为Gerdes 的一本著作撰写的前言(Gerdes,2001 年)
图4.9:根据非洲沙曲线图案推导出的矩阵
可以将两个这样的矩阵相加,从而形成一个新的模式(图4.10)。

图4.10:矩阵加法和色彩图案
格德斯研究过一种特殊的安哥拉Lunda 图画,他以自己女儿的名字将其称为「Liki 图案」。插图(图 4.11)中展示了这样一个Liki 图案及其相关的矩阵。

图4.11:从非洲沙曲线图案推导出的Liki矩阵
格德斯的Liki矩阵具有以下特性:
1. 沿着边界,每个「主要」网格点(图中粗体黑点)总是有两个不同颜色的相邻方格。
2. 任意相邻的两个「主要」网格点之间(垂直或水平方向)的四个单位方格中(纵向或横向)之间的四个单位方格中,相邻的两个方格总是一种颜色、 而另外两个则是另一种颜色(图4.12)。

图4.12:Liki 属性示意图
根据Gerdes的观点,这两个性质意味着正方形利基设计是由循环组成。下面以网格点数为3×3的Liki 设计为例进行说明 (图4.13)。
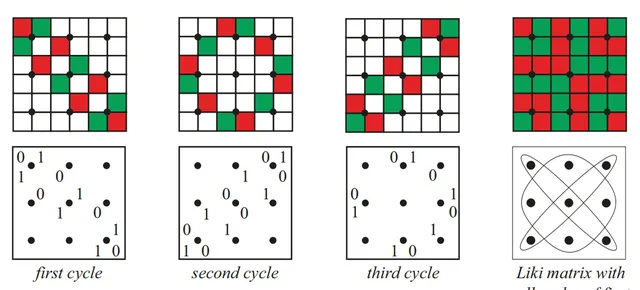
图4.13:Liki 循环
通常的矩阵乘法将这些由0和1组成的矩阵转化为不再包含0和1的矩阵,然而格德斯在这些方形Liki 矩阵中发现了一些非凡的特性(图 4.14)。
图4.14:二阶结构
定理
Liki 矩阵A和B相交: AB=BA.
定理
AB具有二阶循环结构(见插图)。
格尔德斯将这些定理扩展到具有更多光栅点的矩阵,并就这些性质提出了其他变式。这可能是更常见的数学分析在这些沙画上的初步应用。
形式、形状及其分析
一些建筑师和数学家喜欢在古典建筑和绘画作品上画各种矩形、三角形和圆形。希腊神庙、中世纪大教堂或达芬奇的作品都是这些所谓「研究」的最爱。在这种「分析」中起重要作用的是所谓的黄金分割数ϕ(也称黄金分割、黄金比例或神圣比例)。当长度为 x (>1) 的线段被分成长度为 1 和 x - 1 的两部分,并且这种分割使得比例 (x - 1)/1 等于比例 1/x 时,它就出现了。这意味着一元二次方程 x2 - x - 1 = 0,其中 (1 +√5)/2 = 1.6180... = ϕ是正解。长度为 0.618...的较小部分 x - 1 称为小数,长度为 1 的较长部分称为大数。
宽为1、长为ϕ的矩形被称为黄金矩形。发现黄金矩形,甚至在不可能出现黄金矩形的情况下发现黄金矩形,是一些伪科学家最喜欢做的事情。一些雕像的头在很久以前就被砍掉了,但雕像的雕刻者却用黄金分割来解释这些雕像,就好像雕刻者有预知能力,知道雕像的头会被砍掉一样。罗马尼亚外交官马蒂拉·吉卡(Matila Ghyka)是黄金分割神话的煽动者之一,他的弟子们成功地用四种不同的方式为同一神庙制作了黄金分割。在第一幅图中,一些黄金分割大师从较低的阶梯开始,另一些则从第二阶梯开始,或者从第三阶梯开始,最后一些则以神庙的脚为最低点进行绘制(图4.15和4.16)。

图4.15:按照黄金分割定律,左边的矩形「太扁」,右边的矩形「太方」,而中间的矩形是「理想形状」。
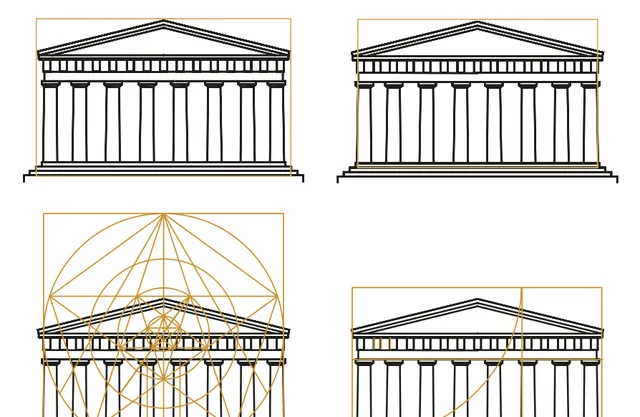
图4.16:在同一栋建筑中「发现」黄金分割的四种不同方法。这说明这些伪科学研究缺乏严谨的方法
各种书籍一遍又一遍地重复着这些图画,却对某些图画相互矛盾的事实毫不关心。面对「在寺庙上画一个黄金矩形」的练习,学生只有在与考官的观点完全一致时才能通过考试。缺乏批判性思维可能是由于这些说法似乎具有可接受性。它们似乎强调了希腊古典文明、文艺复兴以及(部分)实际西方文化的重要性。通过发现艺术表现形式中反映出的有理有据的思想证明,黄金部分有助于支持欧洲优越性的假象。在1984年重新出版的一本带有豪华彩色封面的书中,法国作家D. Neroman认为希腊雕像是理想中的美,而非洲人和犹太人则「尚未成熟」,因为肚脐的高度与肚脐和头顶之间距离的比例小于黄金比例(图 4.17)。

图4.17:尼罗曼对希腊、非洲和犹太妇女肚脐高度的研究,以及具有大小比例的塞努弗雕像
不幸的是,其他人对这一神话的反应是类比地「发现」非洲艺术中最奇妙的黄金分割。他们以同样的创造力,在非洲物品中发现了金色的矩形和主次线段。当然,这并不难,因为非洲艺术和西方艺术一样,也可以运用类似的幻想。另一方面,这也是值得赞赏的,因为艺术头脑对数学启发的主题乐此不疲是相当罕见的。然而,这与科学或数学无关。此外,对于新兴的民族数学领域(该领域本身仍饱受批评)来说,在这种险恶的道路上误入歧途是非常不明智的。
数学书籍中的非洲图形
对非洲艺术形式的研究并不流行,因为人们普遍认为非洲艺术只是感性的(不管这意味着什么)。这种观念的根源或许是非洲人在20世纪60年代初发出的感叹:「欧洲给了我们理性,非洲给了我们情感。」如果这句话是正确的,那么它将支持这样一种观点,即非洲的艺术表现形式几乎纯粹是感性的表现,而欧洲的艺术则更多地基于理性的思考。这种偏见仍然占主导地位,可能阻碍了许多人对非洲雕塑采取技术起草的方法。我们在此不讨论这种说法,因为下面的例子清楚地说明了相反的情况是完全可能发生的。
【数学教师】是美国国家数学教师委员会出版的一本杂志,曾刊登过一些非洲插图 (Zaslavsky,1970年)。该杂志强调了创造性与数学教学之间的关系,并将形式与特定的数学曲线进行了比较(图4.18和4.19)。
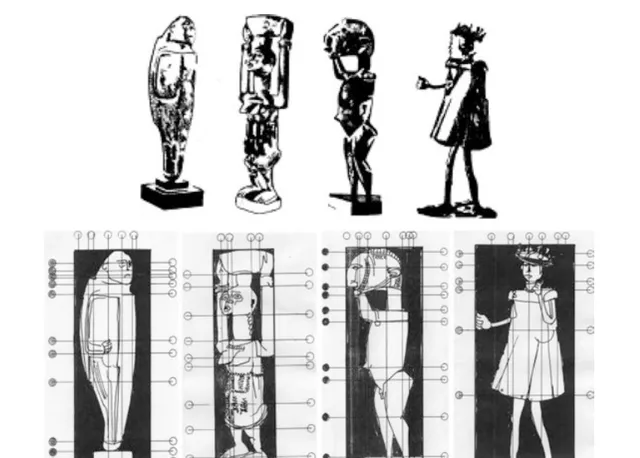

图4.18:卢旺达Nyundo艺术学校使用的合理形式分析示例

图4.19:来自杂志【数学老师】的两幅插图
来自雅温得的Njock教授是一位非洲科学家,他对数学和艺术对非洲大陆的重要性持有强烈的看法(Njock,1976 年,1979 年):
非洲艺术为世界打开了黑非洲社会和文化历史的基本视角:它塑造了两千多年的历史。[……]纯数学是一门创造和想象的艺术。因此,黑艺术本质上是数学的。事实上,它刺激整个人格,道德和认知的可能性,想象力和创造性的态度。在分析黑艺术的贡献时,人们不能忽视个人的知识,或者无数的情感和想象。[…]
公认的教学理论指出了想象力和欣赏的巨大好处。人们最终会想到教育者所允许的自由艺术表达的重要性,通过自发的活动表达自我和强调每个人的独创性的必要性,证明人类思想的创造性进化的重要性,不仅作为艺术活动的基础,而且作为人类生活的一个方面。黑艺术是宇宙文明宏伟结构中最重要的部分之一。
几何图案
有些编织物的灵感似乎来自数学。加纳的阿散蒂人在编织品中大量使用几何图案,象牙海岸和布基纳法索也有许多类似的编织品(图 4.20)。

图4.20:西非的织布机和缝纫机精细编织的织物
这里也有描述织物及其特殊名称的故事。因此,「之」字形边线意味着旅行者将永远回家。不过,这些图案并不总是从几何图形中获得灵感,而往往是出于简单的实用性。例如,它们通常是在小型织机上织成的,这可能就是阿散蒂织品的飘带的由来。之后,它们被简单地缝合在一起,形成较大的织物。一个有趣的现象是,现代非洲纺织品仍在模仿这些条纹图案,尽管如今它们是一体成型的,因此没有与小条纹相关的技术要求(图 4.21、4.22、4.23 和 4.24)(Pauwels,1952年)。

图4.21:模仿条纹图案的现代阿散蒂布料

图4.22:带有抽象装饰的卢旺达小屋内景

图4.23:Pauwels的卢旺达绘画清单;数字表示相关说明

图4.24:卢旺达的传统伊米贡戈画
在国际上,阿散蒂的绘画是最著名的,尽管它们在声誉上可以与南非的绘画相媲美。在中非,许多图画和图案也可以在小屋周围的围栏上、篮子上、盖子上、牛奶罐上和鼓的装饰品上找到。
「纯粹的"绘画
比利时数学家塞利斯在卢旺达逗留期间曾想过,为什么几何图形、非具象图画比人物和动物图片或故事插图更受欢迎(Celis,1972年)。他特别在该国东南部的一个偏僻地区观察到了这一现象。该地区过去交通不便,因此人们认为大多数图画都是原始的传统概念,而不是与其他文化交流的结果,也不是持续文化融合的结果。
用所谓的伊米贡戈装饰小屋的现象似乎可以追溯到大约300年前。口述描述了传说中著名的卡基拉·卡·基梅尼(Kakira ka Kimenyi)如何引入装饰小屋墙壁的传统(图 4.25)。
图4.25:上图中的图案
卡基拉·卡·基梅尼(Kakira ka Kimenyi)一生中的许多事迹表明,他对纯洁的理念非常痴迷;他的牛被关在小屋里,也在那里宰杀,这样就不会有苍蝇飞到它们身上[......]他讨厌泥泞,在大雨中坐在石头上。他的整洁是如此传奇,以至于 「isuku ni ya Kakira 」或「像 Kakira一样整洁」成了一句谚语。
卡基拉拥有丰富的创作经验,他制作这些画作的目的无非是为了自己欣赏和保持整洁;他先是为父亲制作这些画作,[......]然后又为自己的小屋制作这些画作。[......]他自己画了这些画后,鼓励贵族少女们模仿他的想法。就这样,画作流传开来。
G. Celis 和 T. Celis 注意到,他们遇到的所有图案都是由几种基本结构组合而成的。垂直和水平方向,加上三条斜线及其与垂直轴的对称方向,就足以构成所有图案。有了这八个方向,「伊米贡戈 」就可以简化为几种情况,只有平行线、菱形、等腰三角形和等边三角形起作用。
巧合的是,这些几何观察结果导致某些图画因没有遵循规定的规则而被视为非原创而遭到拒绝(见第12章)。还有人利用卡基拉规则为计算机编程,从而创造出传统上正确的图案。具有讽刺意味的是,以纯粹著称的Kakira ka Kimenyi偏爱抽象,却为数学这门「纯粹」的科学做出了贡献。
饰带图案与晶体学
J. 威廉姆斯为使用中国、阿拉伯和非洲绘画来教授6-16岁的学生辩护:
晶体学研究的是按照对称组别对图案进行分类,但多文化图案和设计实例也能说明这一点。扎斯拉夫斯基复制了一幅刚果巴库巴人的刺绣布(现藏于大英博物馆),其中完整地收集了7种不同的一维饰带纹(即希腊神庙上的条状线形图案)。这些图案与一维变换有关,如 180°旋转以及水平和垂直反射。利用群论可以证明,这样的图案只能存在7种。
使用所谓的群论是一种更加数学化的欣赏非洲几何图形的方法,而不是对各种图画进行简单的描述性清点,解释它们的形状、目的或解释。例如,数学家可以利用群论证明,就图案的对称性而言,只有7种饰带图案是可能的;如果图案中允许有一种颜色,那么可能性就会增加到24种。至于(非彩色的)二维图案,即平面图案,则有 17 种数学图案是可能的。D. Crowe 研究了刚果巴库巴人和贝宁人艺术中的重复图案(Crowe,1975 年)。在饰带图案中,他发现了所有7种可能性的例子,但在平面图案中,17种可能性中只有12种(图 4.26)。
图4.26:在贝宁可以找到所有7种数学上可能的饰带图案
非洲分形
在流行数学中,分形是众所周知的,这可能是因为它们可以用漂亮的图画来表示,让人联想起云朵、蕨类植物、菜花或迷幻MTV视频的形状。这一概念已有100多年的历史,但多亏了法国人 B. Mandelbrot(移居美国),这一数学课题才得以摆脱数学象牙塔的束缚,得到媒体的充分关注(图4.27和4.28)。
图4.27:这种分形是为了纪念Benoit Mandelbrot而命名的,他在媒体中普及了这个话题
图4.28:描述【非洲分形:巴伊拉聚落的分形解释】一书的插图
就像蕨类植物的叶子一样,分形也有这样的特性,即放大后的新图像与原图像一模一样。这种放大一直到无穷大,因为对于分形来说,较小尺度上的图画的定义来自较大尺度上的图画。这就是为什么分形的「触角」看起来越来越小的原因。当它们或多或少地覆盖平面或填充空间时,就会产生所谓的分形维度。对于表面上的分形曲线来说,这个维度介于1(直线)和 2(表面的维度)之间,而对于空间分形来说,这个维度介于2和3(空间的总维度)之间。例如,在一件非常保暖的毛衣中编织的线当然是一维的,但它却形成了一个几乎是二维的交错曲面。分形似乎可以用非常简单的数学表述来描述自然现象。
著名的非裔美国科学家本杰明·班奈克(Benjamin Banneker)使用了一种所谓的五边形分形。在塞内加尔,经常可以看到这种分形图案作为装饰出现在脖子上的小皮包上。埃塞俄比亚的十字架是重新发现数学分形结构的其他例子(图 4.29)。
图4.29:塞内加尔皮包上的班奈克分形(上图)和埃塞俄比亚十字架上的班奈克分形
不过,要在非洲人的发型或雕像上看到分形,还需要更多的想象力。当然,只要这些分形在算术和几何上是正确的(前面提到的黄金分割之谜就不是这样),这样的练习就没有什么问题。罗恩·埃格拉什写了一整本关于非洲分形的书。可以说,许多非洲图形的灵感都来自大自然和生活场景,因此这些图形都包含了大自然的分形结构(图 4.30)。
图4.30:用分形解释非洲雕像
另一方面,大卫·阿夫尼尔(以色列耶路撒冷希伯来大学)等科学家已经证明,自然界的分形属性是值得商榷的:很多时候只有两个或三个尺度层次,而无限延续的可能性是分形定义的一部分。在埃格拉什所谓的非洲分形中,通常也最多只有三个层次。阿夫尼尔甚至亲自写信给曼德布罗特,反对他对自然的分形解释。他们的讨论没有得出明确的结论。帕特里克·福勒(Patrick Fowler)在私人信件中说了一句风趣的话: 「为什么没有一本关于'天主教分形'的书呢?因为在某些宗教艺术中,圣人手捧圣母玛利亚像,怀抱耶稣圣婴。那也是分形艺术吗?这样的雕像能证明天主教艺术家在600年前发明了分形吗?同样,也许还有印度教或维京人的分形(图 4.31)。
图4.31:天主教、印度教和维京人的民族数学分形
因此,无论如何,这里有一个沙子曲线、绘制图案和分形优雅交汇的例子。格 德斯运用数学想象力,从非洲沙地曲线出发,首先将其转化为绘画图案,从而得到了一个分形(图 4.32)。
图4.32:由简单沙粒曲线图案得到的格德斯分形
青山不改,绿水长流,在下告退。
转发随意,转载请联系张大少本尊。











