这篇文章是给中学生看的,我发现很多中学生纵使能知道分数、小数各自的集合范围,但理解停留在表面。我想通过两个证明来更加明确各自的内涵。「分数」这个名词取得就很本质,把整数平均分成几份儿就是分数。分数和整数构成有理数,无理数即不能表示成整数或分数的数。用两整数之比就可以表示所有有理数。那么有理数就可以由整数来构建。那无理数能用有理数来构建吗?大学的【数学分析】就是用有理数的极限来构建的实数。「小数」这个名词就透露了「极限」,这种数的表示天然的给了你一个收敛数列。比如π=3.1415926......,它天然的给了你一个数列{3, 3.1, 3.14, 3.141, ......},这个数列就收敛到π。小数可以表示分数,也可以表示无理数,能表示成分数的小数是有限小数或无限循环小数。很多中学生只知道这个结论,但不知道原因。现在就给出两个命题来证明。
命题1 : 无限循环小数是分数。
证明 :设a是一个无限循环小数,从小数第n位开始出现循环节,循环节长度为m,那么
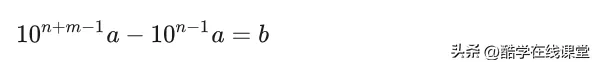
b是一个整数,则

证明了a是一个分数。举个例子,有无限循环小数a=3.15616161......,100a=315.616161......,10000a=31561.616161......,则
10000a-100a=31561-315
于是a是分数。
命题2:分数是有限小数或无限循环小数。
证明: 假设a是一个分数表示成a=m/n,m,n是正整数,且n不等于0。设m除以n,商为x1,余数为r1,r1<n, 10*r1除以n的商为x2,余数是r2,r2<n,这样一直进行下去,存在两种情况,情况一是,存在t,使得

情况二是,根据抽屉原理,一定会出现一个余数与之前的余数相等,假如

则a=m/n表示成小数对于第一种情况是

对于第二种情况是
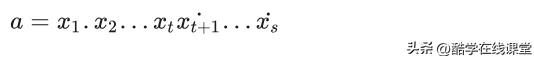
这样就证明了分数是有限小数或无限循环小数。
根号二是无理数,所以它表示成小数是无限不循环小数。根号二是无理数的证明方法早在古希腊的欧几里得时期就已经出现,即用反证法假设它是分数,推出矛盾。假设

推出a,b都是偶数矛盾。
小数这种数的表示在证明实数的性质时用的比较多,比如前面写过一篇【证明实数不可列】,就是用的小数的表示形式。











