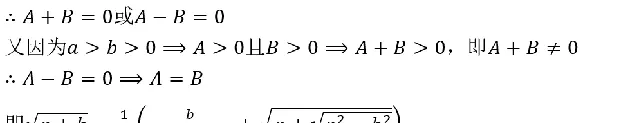注:本文中证明的是繁根式内含根号的项是正数的化简方法(形如√(a+√b)),若要化简根号的项是负数的请看置顶评论
本文含推导和证明两部分
本文中的字母无特殊说明,则均表示某实数
一、推导
首先,

而事实上,由于m=b/(2n),所以若n<0,则m<0,而由于a>b>0,所以√(a+b)=m+n>0,因此取n<0的根不满足题意,所以取
因此,
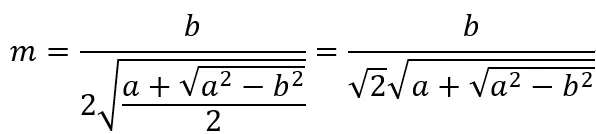
所以,√(a+b)=m+n=
我们发现,有一项√(a+√(a^2-b^2)),而若将他代入上方的化简方法,得到的结果会含有√(a+b)
(也就是说,回到最开始的式子了,即√(a+√(a^2-b^2))无法代入上方式子再次化简,否则会变回原来的样子)
因此,若√(a+√(a^2-b^2))不是繁根式,则√(a+b)可化简,否则不能被化简
为方便,令√(a+√(a^2-b^2))=t,再提公因式,可以把式子变得更简便好表述,如下:

注意,如果含根式的项<0,如√(28-10√3),可以设√(a-b)=m-n,然后使用与本文类似的方法推导
以上推导,以下是反向的证明(实际上有了推导,这个式子就是正确的了,不过反向证明同样有趣,利用了平方差公式等)
要证明:

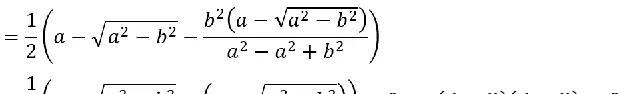
接下来,只要证明A+B≠0,则A-B=0,即A=B