
粒子可以用向量空間中的向量表示,某種程度上是所有可能測量結果的疊加。物理量(如能量、位置等)則由該空間中的線性算符表示。
既然要使用線性代數的框架,我們應該確保對 什麽是向量空間 有紮實的理解。讓我們看一下向量空間的數學定義。正式地,向量空間是一個滿足以下規則的物件集(稱為向量):
對於任何向量 u,v,w 和純量a,b:
大多數規則只是規範我們已經直觀理解的概念。比如,第一個規則僅僅說明,兩個向量相加得到另一個向量。下一個規則指出,向量乘以純量也會得到另一個向量。而其余的很多規則只是加強了我們對向量如何相加和如何與純量相乘的直觀認識。
那麽以這種方式定義向量空間的好處是什麽呢?這種定義沒有提到數位列或箭頭。
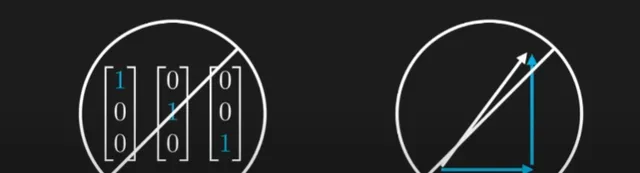
任何滿足這些規則的物件集,都可以形成一個向量空間。只要規則正確,它可以是水果,可以是函式,當然也可以是我們熟悉的數位列和箭頭。 希望你開始明白線性代數和向量空間更多是關於 結構和模式 ,而不是關於你使用的物件型別 ——恰好向量空間的這種結構正是我們描述量子世界所需的。
既然我們理解了什麽是向量空間,讓我們將其套用到量子力學中。我們希望用向量空間中的向量來表示粒子。
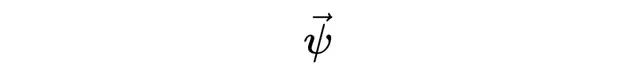
更具體地說,向量空間中的向量代表一個 量子態(quantum state) 。 量子態是一個數學物件,它包含了粒子的所有物理內容。 從中我們應該能夠提取出在特定時間下可能的位置、動量、能量等以及所有相關的 機率 。
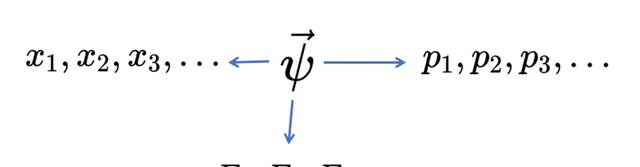
在量子力學中,物理學家喜歡用不同的符號來表示向量。我將使用這個符號來表示向量:
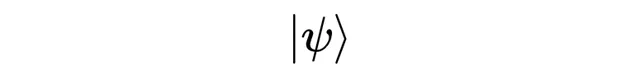
當以這種方式寫一個向量時,我們稱它為「ket」。它仍然是一個向量,只是符號不同。選擇這個符號的原因可能看起來奇怪,但它的威力將在後續文章中顯現。
現在讓我們將這個符號與量子力學聯系起來。前面一篇文章中,我們想用所有可能測量結果的線性組合來表示粒子,例如能量。因此,會有一個代表每個可能能量結果的量子態「ket」的列表,當前的量子態由這些量子態的線性組合(通常稱為疊加)表示,
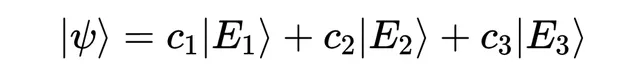
而系數與該結果的機率有關。如果我們想測量角動量,就會有一個代表每個可能角動量結果的量子態「ket」列表,並且會有一個不同的線性組合,
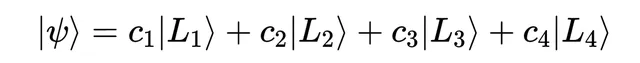
但當前的量子態仍然相同。對於可以進行的每一個測量,情況都是如此。
現在我們有一個有限的結果態列表,但很有可能有無限多的結果。
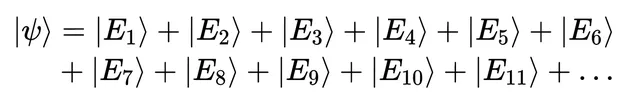
想一想,有什麽能阻止你給粒子越來越多的能量呢?我們需要為任意高的能量準備能量結果態。因此,有時我們可能會有無限多個「ket」的線性組合,代表無限多結果的疊加。 後面,我們將簡要討論這種無限帶來的一些問題(以及為何希爾伯特空間可以解決這些問題) ,但現在我們假設無限線性組合不會引發任何問題。
然而,有另一個問題需要解決。到目前為止,我們討論的是當像能量和角動量這樣的物理量有離散的一組可能值時的情況。但物理量並不總是離散的!例如,位置。目前,沒有實驗證據表明位置是離散的 ;電子可以出現在任何地方——沒有「列表」可以表示所有可能的位置。 換句話說,位置是連續的(continuous),而非離散的。我們希望能夠在理論中以數學方式描述這一點。
所以這裏有一個難題:假設電子可以擁有任意可能的位置(盡管有些位置可能比其他位置更可能)——我們如何使用可能位置的「ket」來表示電子的量子態?典型的求和不夠用了,因為進行求和需要一個 離散的 列表,而要覆蓋所有可能位置是不可能的,即使列表是無限的。
因此,我們需要一種能夠對連續集進行求和的數學運算。你可能已經意識到,積分正是這樣一個運算。
所以讓我們利用積分,在可能結果是連續集合時構造線性組合。首先,我們想將其寫成一個和,因此寫下積分符號來表示一個和,
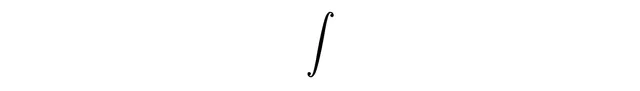
其中上下限預設為正無窮大和負無窮大。接下來,在所有可能的位置結果上求和,用變量x表示,因此需要一個微分dx來表示這一點(不用擔心dx放在哪裏,在許多理論物理文獻中你會看到它放在前面)。
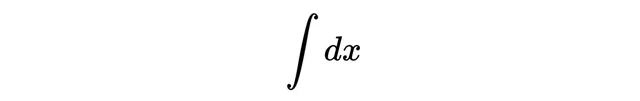
接著,我們需要「ket」,將它們按它們所代表的位置x來標記。
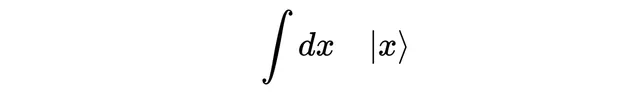
最後,我們需要系數。對於每個可能的位置x,都有一個系數,這意味著需要一個對應於每個x值的數,這正是函式的作用,所以我們使用一個函式來作為系數。
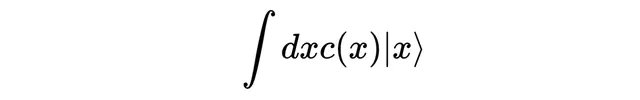
這樣就完成了!我們寫出了一個量子態,其中疊加的是一組連續的結果。
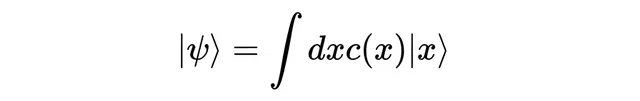
如果你第一次看到這,可能會感到非常困惑。只要記住積分代表一個連續求和,因此這只不過是一個連續的結果態「ket」的線性組合。
繼續之前,我想花一點時間討論這裏的「系數函式」。用函式代替系數可能看起來很奇怪,所以讓我們看看它是如何形成的。假設位置確實是離散的。在這種情況下,將有一組可能的位置結果及其相關系數。
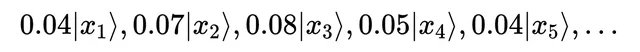
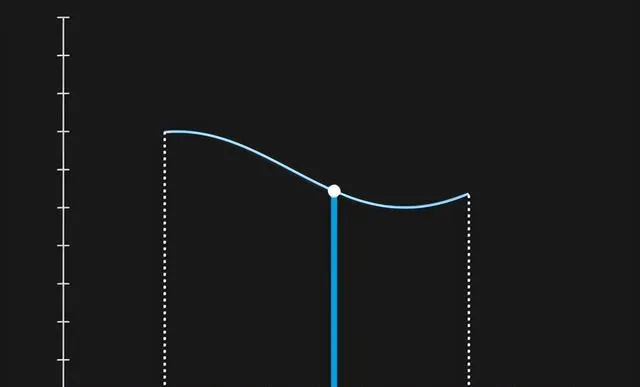
讓我們將這些系數作為它們對應的位置的函式進行繪制。對於每個離散位置x,將它的系數c作為一個點繪制出來。
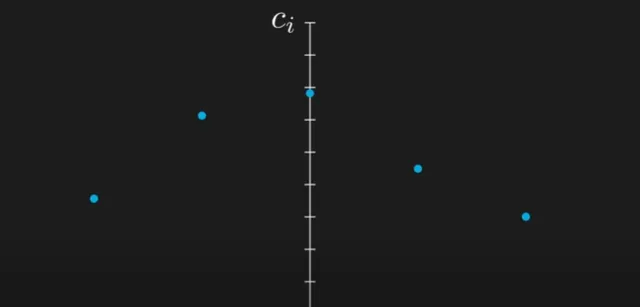
現在,讓我們「解除」位置的離散性。讓可能位置之間的間隙縮小,填補所有缺失的位置系數。隨著這一過程發生,系數開始變得越來越接近,
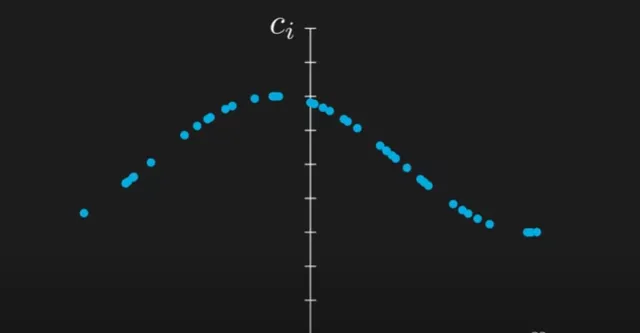
你會看到它們最終形成一條線——換句話說,它們開始形成一個函式!只是假設這個函式必須是連續的 ,但我們將在以後的文章中證明這一假設。這就是我們是如何從離散系數過渡到函式的?
讓我們繼續並註意到一個重要的事情。記住,在可能結果的線性組合中,系數與獲得該特定結果的機率有某種關聯。 這意味著這裏的函式某種程度上告訴我們關於某個位置的機率。 如果你有一些量子知識,也許你知道有一個與位置機率相關的函式——波函式!事實上,這裏的函式就是波函式。
所以,希望你看到線上性代數框架中,位置波函式只是每個可能位置「ket」前面的系數列表。當我第一次學習量子力學時,我一直在想函式如何與線性代數框架聯系起來,現在希望你能明白了。很多人常說波函式是一個向量;盡管函式可以存在於它們自己的向量空間中(你可以以這種方式構建量子力學),但現在你知道波函式實際上代表什麽了。 在量子力學中,波函式表示每個連續「ket」列表前面的系數。
那麽這些系數與波有什麽關系呢?為了解釋這個問題,我們必須推匯出薛丁格方程式,但這是後話了。
總結一下:在這個模型中,粒子用向量空間中的向量表示,也稱為量子態。我們為這個向量選擇了一種特殊的符號,稱為「ket」。這個「ket」包含了粒子所有的資訊。對於任何物理量,量子態都是所有可能結果「ket」的線性組合(即疊加),系數告訴我們該結果的機率。如果物理量有一組連續的結果,我們用積分代替求和,用稱為波函式的函式代替系數。











