中國古代數學幾何從誕生,就是圍繞著「用」——測算天道之「用」在發展。
從【周髀算經】,一直到清代江永的【數學】、杜知耕的【幾何論約】、黃百家的【勾股矩測解原】……;從勾股定律到矩陣、弧矢推算,從劉徽的割圓術到祖沖之的綴術……無不是為天道推算而服務的。
而天道推算的結果呢?在文字不夠發達的上古,總是以圖像——八卦的形式在陳述。
這就意味著數理化天賦不高者,是學不精易學的。
為什麽呢?
因為除了易歷推算不給力,就光平面、曲面與空間之間的翻轉,就能讓數理化天賦不高者翻的暈頭轉向。
因為中國的數學幾何作為易歷推演的工具,她和西方傳統數學幾何是不同的。
西方傳統的數學幾何是平面幾何,也叫歐氏幾何。
而中國數學幾何從萌芽,就是空間幾何,曲面幾何,屬於非歐幾何。
所以在學習易學的過程,關於平面、曲面和空間的翻轉能力至關重要!
為什麽呢?
咱們先看一下歐氏幾何和非歐幾何的區別
如果我們把眼睛當成微分器,歐氏幾何都是被眼睛微分後的平面幾何學,就像我們上古時代的地平座標,都是受視野限制下的認知。
而歐氏的兩條平行線永不相交論,正是視野局限下的公理。
也就是說,歐氏的兩條平行線,之所以平,之所以直,之所以不相交,都是源於我們視野的局限。
如果我們站在整個宇宙視野裏,看歐氏在地球上畫的那兩條平行線,其實都是附在地球面上的曲線。
如果這時候,我們再回到地球平面上看,隨著視野的差小,歐氏的兩條線,又變成了兩條永不相交的直線。
正是這個原因,時過數千年,走到黎曼時代,西方幾何學圍繞著視野問題,發生了一次變革。
也就是說,黎曼面對歐氏的兩條線,做了一次視野和視角的轉換,從歐氏的地平面轉向了宇宙,於是歐氏的兩條平行線,就變成的地球的兩條經線,得出:平行相交論。
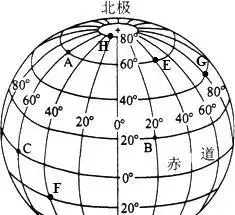
就這麽簡單,黎曼就得出了平行線相交論,開創了非歐幾何。(附論:黎曼在曲面上提出這一論點時,忽略了一個問題,那就是和緯線平行的線,無論在曲面上如何空間化,都是是符合歐氏不相交論的 。 )
我為什麽要講這段西方幾何的歷史變革呢?
因為中國數學幾何從誕生,研究物件都是天道——曲線、曲面和空間。
也就是說,因為中國數學幾何從誕生就是空間幾何,是圍繞著曲線、曲面在發展的非歐幾何。
所以,作為天文歷算影像表達的八卦,剛一入門就考驗著初學者從平面到曲面、從曲面到空間的翻轉能力。
這個能力是學易的天賦基礎!
比如我昨天講的:陰陽太極圖就是七衡六間平面圖的空間圓圖,可就是最基本的一翻,讓很多讀者都翻迷了,紛紛留言表示質疑。
為什麽呢?就是這些讀者缺失學易的天賦基礎,缺失從空間到平面、從平面到空間互相轉換的基本能力。
再比如勾股定律,勾股定理其實就是把太陽的周天圓運動的黃經度(八卦的圓圖),利用圭影的長短以及直角三角形,進行了平面化的推演。如果連這一點最基礎的內容都翻不過來,如何學國學呢?
也就說,圍繞著天道推演為中心的中國文化,不是文科,而是理科,所以我並不建議數理化天賦不高者學易、學醫,因為光空間、曲面、曲線、直線和平面之間的翻轉,就能把你翻到暈頭轉向。











