那麽在太陽的重力下,為什麽月球不脫離地球的重力獨立運轉呢?
地球對月球的重力是2.5倍的原因又是什麽呢?
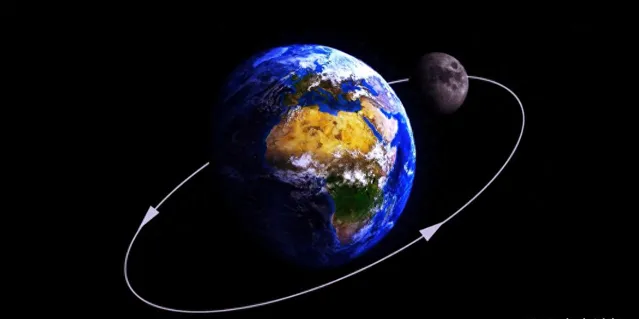
其實月球不脫離地球重力獨立運轉是有原因的,下面我們就來一探二者重力大小的奧秘!
作為行星家族的一員,地球與月球的執行狀態由太陽的重力所決定。
太陽作為太陽系的中心,擁有恒定的重力,位於行星家族的中心位置,如同巨大的吸盤吸引著行星家族的所有行星向自己靠攏。

那麽在太陽的重力作用下,它會對地球和月球產生什麽樣的影響呢?
在太陽的作用下,地球免不了會受到太陽的重力影響,但不同時間受到的重力大小也是不同的。
這是因為地球在軌域上不是固定不動的,處於不斷運動的狀態,同時按照克卜勒三定律,行星與它的中心之間的吸重力與行星與中心之間的距離平方成反比。

地球在繞太陽運動的過程中,駛離太陽的距離也會有所增加, 所以此時地球受到太陽的重力並不是很強。
而地球在軌域上它的速度是非常快的,隨著太陽的重力加速的駛向太陽,到了最近距離的時候,地球將會受到最大的重力。
而此時地球的速度已經非常快了,它的向心力也非常大,如果地心力沒有受到太陽重力的物理作用,地球就會直接飛出太陽的重力範圍,但是地心力受到太陽的重力的約束,所以地球就會繞太陽做圓周運動。

太陽的重力對地球來說是非常的重要,那麽對於月球呢?
由於在太陽系中,月球比較特殊,它就跟隨著地球一同繞太陽運動。
在太陽的重力作用下,月球不僅受到地球的重力約束,還需要克服太陽對它的重力,而且太陽對月球的重力是地球對月球重力的2.5倍,所以月球繞地球運轉是一件自然而然的事情。
那麽地球對月球的重力為什麽是2.5倍呢?
要解答這個問題就需要從行星的重力公式來進行推導!

重力公式是由牛頓提出的,他透過實驗和數學模型的數學運算式得出了重力公式:
F=GM1M2/r^2;
式中:G是萬有重力常數,值為6.67*10^-11 N·m^2/kg^2,是一個恒定數值;
M1是第一個物體的品質;
M2是第二個物體的品質;
r是兩個物體之間的距離;
F是兩個物體之間的作用力。

根據重力公式,我們可以得出:
重力大小與兩者之間品質的和成正比;
重力大小與兩者之間的距離平方成反比。
根據上述公式,我們可以得出太陽對地球的重力大小與太陽對地球的重力大小有所不同。

太陽對地球的重力大小:FD=GM太陽M地球/r^2;
而如果計算太陽對地球的重力大小的時候:
太陽的品質:1.9910^30kg;
地球的品質:5.9810^24kg;
太陽和地球之間的距離是1.4910^11m;
將這些數據帶入重力公式中進行計算,可得出:FD=3.5310^22N。
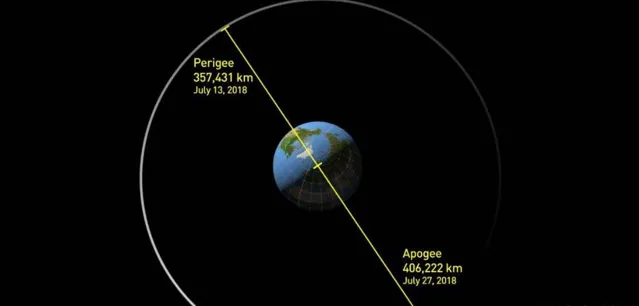
太陽對月球的重力大小:FM=GM太陽M月球/r^2;
太陽的品質:1.9910^30kg;
月球的品質:7.3510^22kg;
太陽和月球之間的距離是1.4910^11m;
將這些數據帶入重力公式中進行計算,可得出:FM=1.9810^20N。
M是月球的品質,所以地球對月球的重力:F=GM1M2/r^2;
地球對月球的重力:FED=GM月球M地球/r^2;

將M1和M2互換位置,可得:
FDE=GM地球M月球/r^2;
M地球:M太陽=1:333000;
M太陽=G
M月球;
FDE=FED+FM;
FDE=2.5FM;
FDE=2.51.9810^20N;
FDE=4.9510^20N。
所以地球對月球的重力為4.95*10^20N。
地球對月球的重力是2.5倍,而太陽對月球的重力是地球對月球重力的2.5倍,那麽根據以上的推導,月球是繞地球還是繞太陽運轉。

根據克卜勒定律可知,太陽對行星的重力會讓其繞太陽運轉,而地球對月球的重力是太陽對月球的重力2.5倍,又因為地球在執行過程中不斷變速。
M太陽對地球的重力平方和地球對月球的重力平方之間的大小關系為:
GM太陽M地球/1A^2=2.5GM太陽M月球/B^2;
M太陽,G,1均為恒定數值,所以可以進行約分,整理得出:
A^2=2.5B^2;
A=√2.5B。
太陽對地球的重力是地球對月球的2000倍,地球對月球的重力是太陽對月球的2.5倍。
所以月球是繞地球運轉的,所以月球不會脫離地球重力而獨立運轉。











