在統計學和機器學習中,理解變量之間的關系對於構建預測模型和分析數據至關重要。探索這些關系的一種基本技術是 雙變量投影 bivariate projection 。它依賴於二元正態分布的概念,所以又被稱為二元投影。這種技術允許我們根據另一個變量來檢驗和預測一個變量的行為,利用它們之間的依賴結構,所以在本文中我們統一將其轉譯為二元投影。
二元投影有助於 確定在給定另一個變量的特定值時的一個隨機變量的期望值 。例如,線上性回歸中,投影有助於估計因變量如何隨自變量變化而變化。
本文分為3個部份:在 第一部份 ,我將探討二元投影的基礎知識,推導其公式並演示其在回歸模型中的套用。在 第二部份 ,我將提供一些關於投影的直觀理解和一些圖表,以更好地理解其含義。在 第三部份 ,我將使用投影來推導線性回歸的參數。
1、二元正態投影公式
設 Z 是一個隨機向量,服從正態二元分布 N(μ, Σ) ,其中
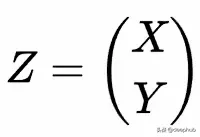
Z的形式中X和Y是服從正態單變量分布的隨機變量
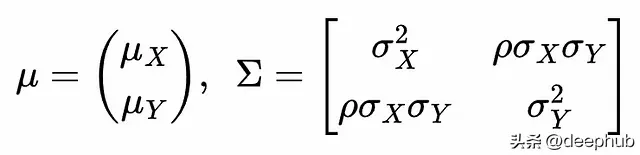
上面公式是Z的均值和共變異數矩陣的形式,用X和Y的均值和變異數表示。ρ是X和Y之間的相關性。
那麽,給定 X = x 時 Y 的條件分布是正態的,由以下公式給出:
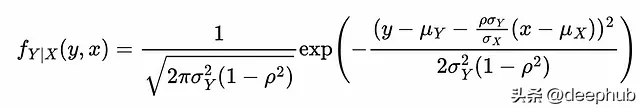
(在文章末尾的附錄會有完整的推導流程)
這是一個正態分布的密度函式,其條件均值為
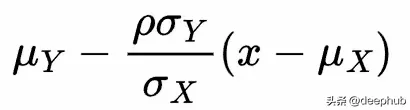
條件變異數為
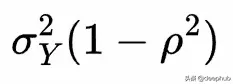
現在我們可以寫出 Y 在 X 上的線性投影 ,即給定 X = x 時 Y 的條件均值:
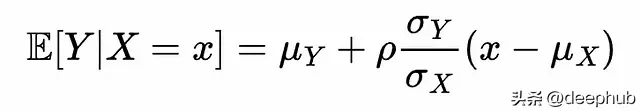
這是 Y 和 X 之間的線性關系,因為它是 Y 在 X 上的線性投影。
這個公式告訴我們什麽?我們可以在實際套用中如何使用它?
2、解釋和模擬
二元投影在預測建模中起著至關重要的作用,它允許我們根據一個變量的值來估計另一個變量的期望值。 這裏將使用線性回歸做一個實際的例子。
除了預測能力外,二元投影還提供了關於兩個變量之間關系的性質和強度的寶貴資訊。二元投影的另一個機器學習套用是檢測異常或離群值。透過投影,這個過程變得更容易管理,因為它突出了變量之間預期關系的偏差。
在使用線性回歸做實際例子之前,我們先執行一些Python模擬,以更好地突出二元正態分布的形式以及透過其投影可以做什麽事情。
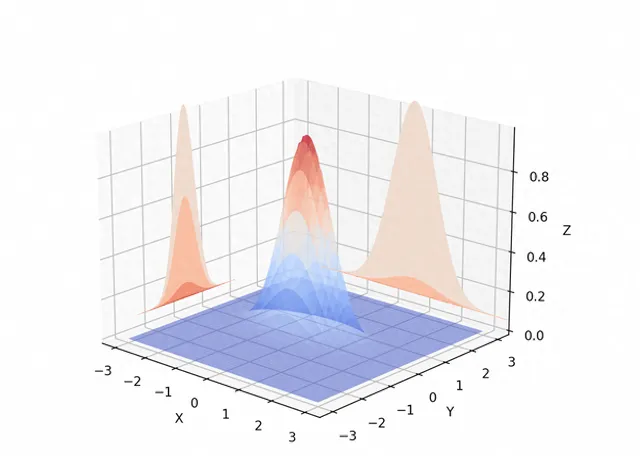
在以下圖表中,隨機變量 X 和 Y 服從標準正態分布 N(0, 1) 。我們將看到當設定不同的相關性 ρ 值時,圖表如何變化。
一個極端情況可能是設定 ρ = 0 ,這意味著兩個隨機變量不相關:
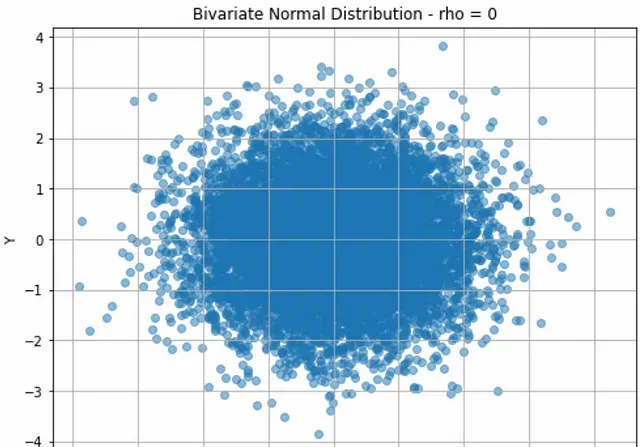
兩個隨機變量以其均值 0 為中心,它們的散點圖呈圓形。這表明變量是獨立的。變量之間沒有明顯的線性關系。下面的3D圖中,可以更好地看到到分布的形式。
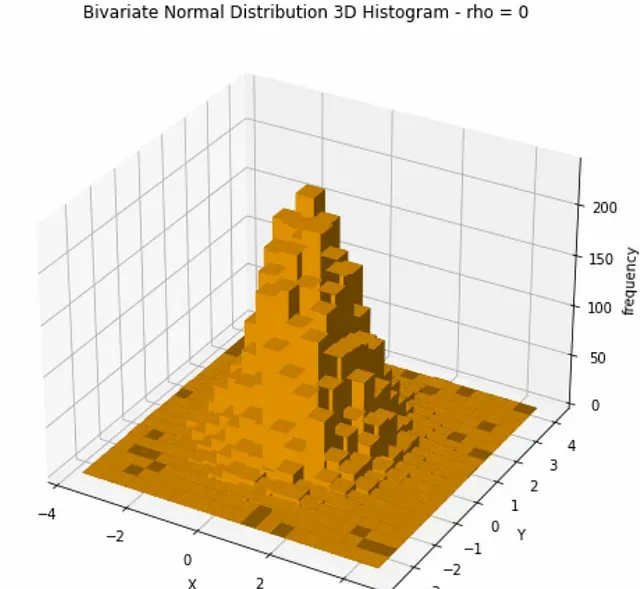
現在讓我們套用投影公式,看看對於不同的 X = x 值, Y 的分布會發生什麽變化。
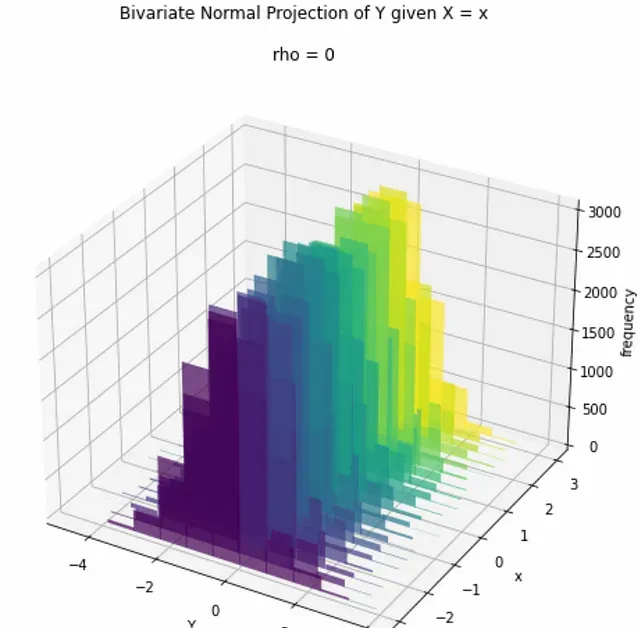
Y 的分布不受不同 x 值的影響。 Y 的均值和變異數卻保持不變。
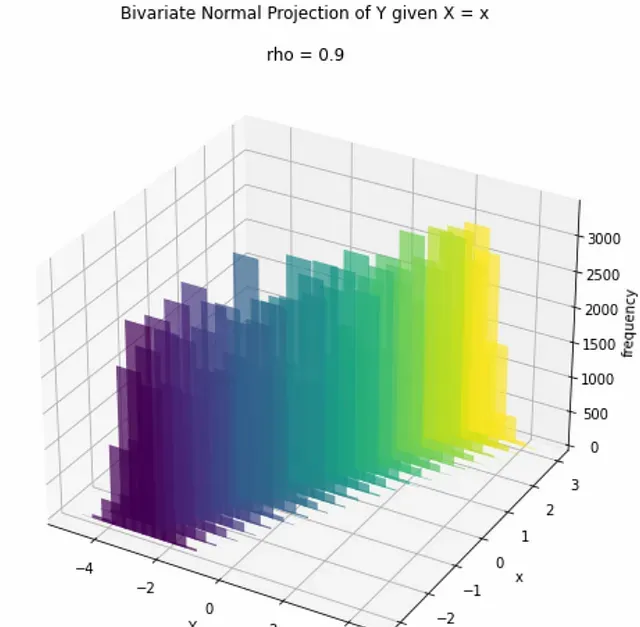
現在讓我們看看對於一個更有意義的相關性會發生什麽。讓我們設定 ρ = 0.9 :
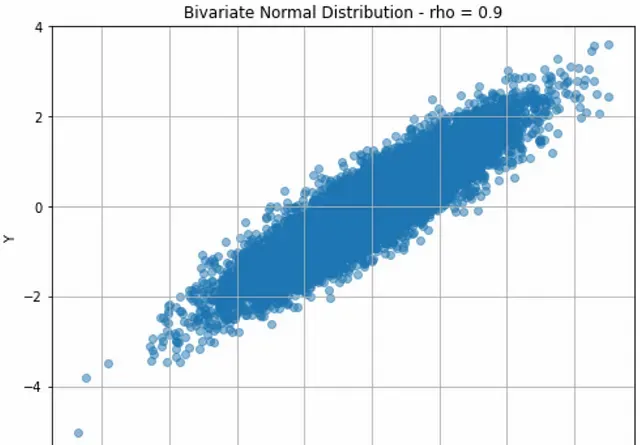
兩個變量的均值仍然以 0 為中心,但散點圖顯示了明顯的線性關系。3D圖如下,可以看到現在分布不再像前面的例子那樣呈現"圓錐"形。
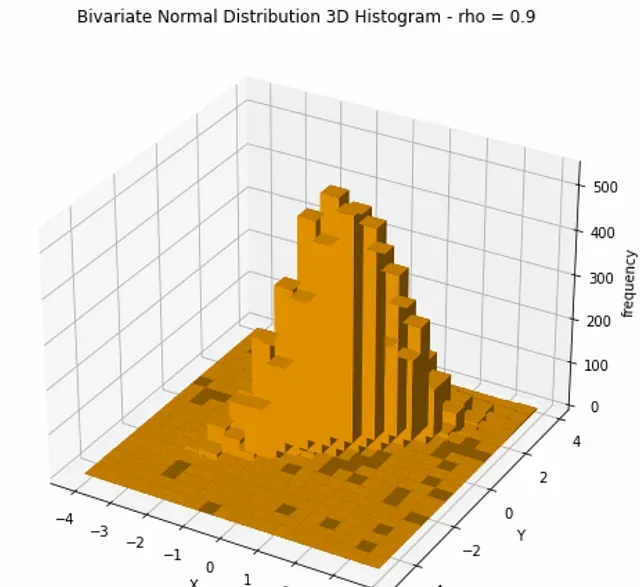
繪制投影,我們現在可以看到 Y 的分布實際上受到不同 x 值的影響。有趣的是, Y 的均值依賴於 x (因為其值取決於 x 和 μ X_ 之間的差異),而 Y 的變異數不隨 x 變化 ,因為它只依賴於相關性 ρ 。此外, 變異數比 ρ=0 的情況小 ,因為它隨 1-ρ² 縮放。
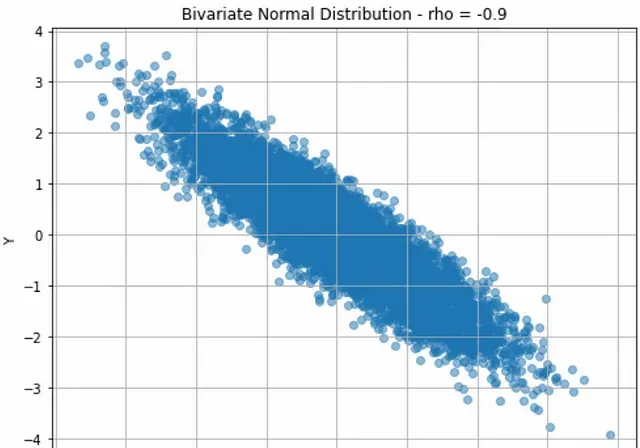
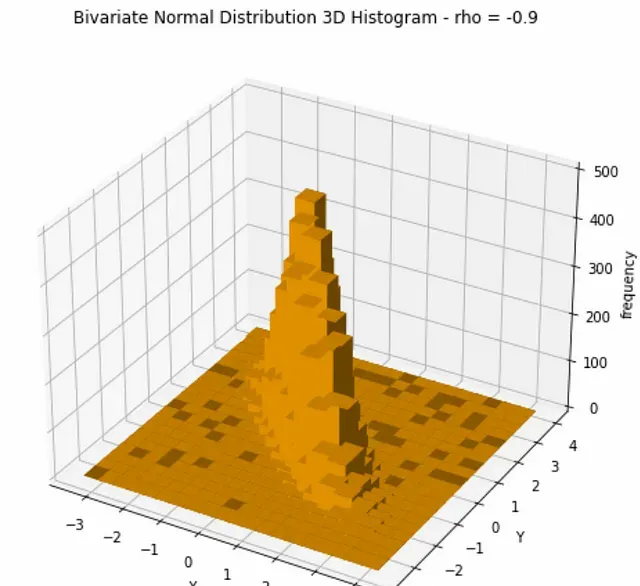
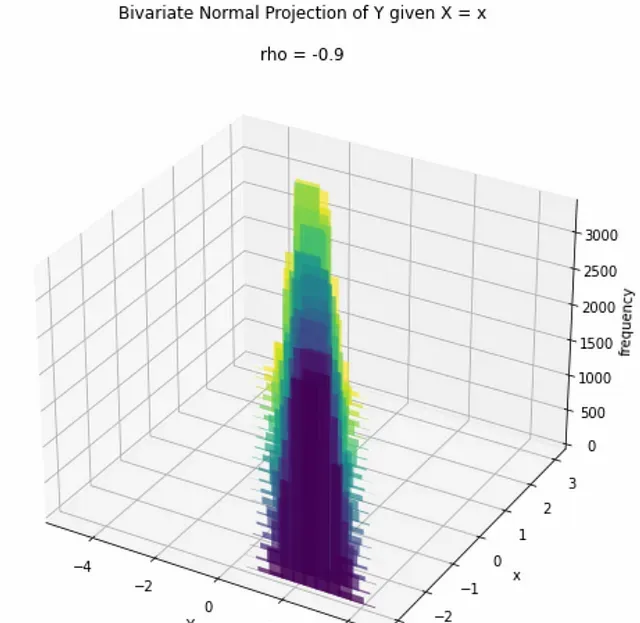
最後一種情況是 ρ = -0.9 與前一種情況非常相似:
3、套用 - 線性回歸
現在讓我們將投影套用到一個簡單的機器學習案例:線性回歸。假設我們想建立一個機器學習模型,使用房屋面積( X 變量)的值來預測房屋價格( Y 變量)。我們有一個包含 X 和 Y 的歷史數據集。
假設變量的分布如下,並且它們有線性關系:
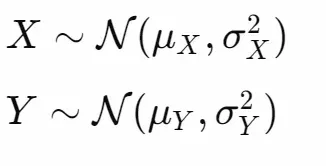
我們建立一個模型,能夠根據 X 的特定值預測 Y 的值:
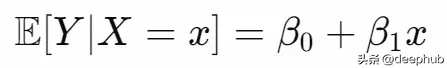
其中beta代表線性回歸的系數,就像通常的情況:
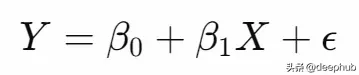
使用投影公式
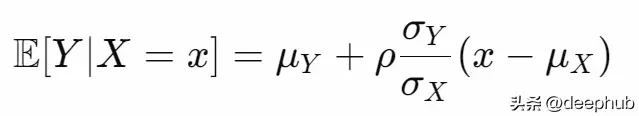
透過這種方式,我們可以使用(從數據集估計的)分布參數來估計線性回歸系數。首先兩個運算式:
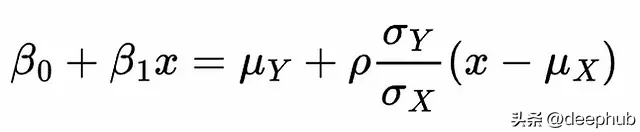
重新排列右側的項,以分離乘以 x 的項和不乘以 x 的項:
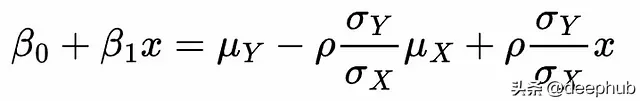
為了使等式成立,參數應該是:
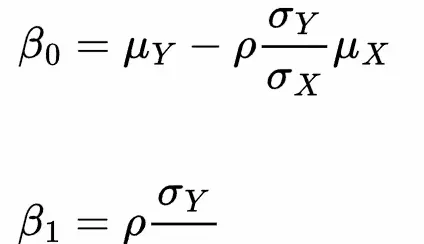
這些就是線性回歸參數的估計量!
附錄:二元線性投影推導
讓我們從定義兩個隨機變量 X 和 Y 的 聯合密度函式 開始:
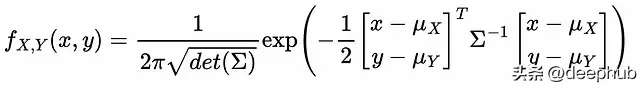
計算共變異數矩陣的行列式:
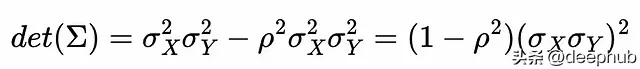
和共變異數矩陣的逆:
將此代入密度函式的運算式,我們得到:
現在,正態二元分布的 邊際機率密度函式 是正態單變量。 X 的邊際函式由以下公式給出:
現在我們可以計算給定 X=x 時 Y 的條件分布。註意,這仍然是正態的:
代入聯合密度函式和邊際密度函式得到投影密度
投影公式現在是給定 X = x 時 Y 的期望,可以透過積分投影密度函式來計算。指數內的二次項可以解釋為隨機變量減去其均值。在這種情況下,均值是 mu_Y 偏移 了依賴於 x 的項。在上面繪制分布時也看到了這種效果。變異數由 1-ρ² 縮放 。
分布的期望值
這就是二元投影的全部退大過程。
總結
線性投影是統計學中一個強大的工具。它的套用非常廣泛,從數據降維到回歸分析,再到訊號處理,線性投影都發揮著重要作用。在數據分析中,線性投影可以幫助我們將高維數據對映到低維空間,從而簡化問題的復雜性,使得模型更易於解釋。線性投影在回歸模型中用於預測和估計目標變量的值。透過這些套用,線性投影不僅提高了數據處理的效率,還增強了我們對數據背後規律的理解。
參考文獻
[1] Joel Hasbrouck (2007). Empirical Market Microstructure, Chapter 7
[2] Alex Tsun, Probability & Statistics with Applications to Computing, Chapter 5.9
作者:Luigi Battistoni











