直接告訴我們,你的速度的確超光速了,因為這就是簡單的速度疊加,小學數學都學過。

但很多時候,直覺並不靠譜,因為我們的直覺是建立在日常生活經驗基礎上得出來的,是以絕對時空觀為基礎的。
何為絕對時空觀?簡單講就是,時間和空間是絕對不變的,任何人對時間和空間的感覺都是一樣的。比如說你的一秒與我的一秒沒有什麽不同,因為時間是絕對的。

但是,愛因史坦告訴我們,絕對時空觀是錯誤的,時空是相對的,這意味著時間和空間具有彈性,物質以及物質的運動都可以影響周圍的時空,結果就是,每個人感受到的時間和空間其實都不一樣。
只不過我們生活在一個低速和低重力世界,很難直觀感受到時空的變化,所以我們會認為時空是絕對的。在亞光速以及強重力世界,時空的變化就比較明顯了。
說了這麽多,或許你應該明白了,你在光速飛船上奔跑,你相對地面的速度並不會超光速,而仍舊會是光速。

當然,飛船的速度也不可能達到光速,所以你相對地面的速度始終會比光速小。這說明了一點,任何試圖透過速度疊加的方式實作「超光速」的想法都是不靠譜的,實際上這種想法本質上仍舊沒有擺脫絕對時空觀的束縛。
你可能會提出質疑:難道我們平時用到的速度疊加公式是錯的嗎?
沒有錯,但也錯了!這樣說並不矛盾,下面來具體講一下。

平時我們用到的速度疊加公式,實際上就是伽利略變換,用公式表達出來就是V=V1+V2。伽利略變換是建立在絕對時空觀基礎上的,所以只適用於低速世界。
比如說,你乘坐一輛高鐵,高鐵的速度是每秒100公尺,你在高鐵上奔跑,速度為每秒5公尺。那麽你相對地面的速度就是每秒105公尺。這個結果很符合我們的日常生活認知。
但是,由於伽利略變換是以絕對時空觀為基礎的,所以它只是個近似值,只適用於低速世界。而一旦來到高速世界,伽利略變換就不再適用了,必須用到勞侖茲變換,愛因史坦也把伽利略變換作為相對論的基本公式之一。

勞侖茲變換考慮到了時間的相對性,所以它不但適用於低速世界,在亞光速世界同樣適用。
從公式中可以看出,當V1和V2很小時,公式中的分母就趨於1,於是公式就簡化為V=V1+V2,就是伽利略變換。所以伽利略變換只是勞侖茲變換在低速世界的特例,也是近似值。
不過如果當V1和V2很大,接近光速時,公式就不能簡化為伽利略變換了。而且,不管當V1和V2多大,哪怕兩個速度都是光速,最終的疊加速度也不是光速的兩倍,而仍舊會是光速。
而且,當V1和V2中只要有一個是光速,最終的疊加速度都會是光速。

如果非要較真的話,上面你在火車上奔跑的例子,你相對地面的速度並不是每秒105公尺,只不過誤差非常非常小,我們根本感覺不到,也不會對我們日常生活有任何影響,即便是火箭發射的過程,也沒有必要考慮時空的相對性,也是以絕對時空觀為基礎的。
那麽,在相對時空觀背景下,為什麽速度不能直接疊加呢?
相對時空觀的一個重要前提是光速不變,也就是光速不變原理,光速是絕對的,在任何參照系下都保持不變,為了保持光速的絕對性,時間和空間必須做出「妥協」,不然光速就是可變的。
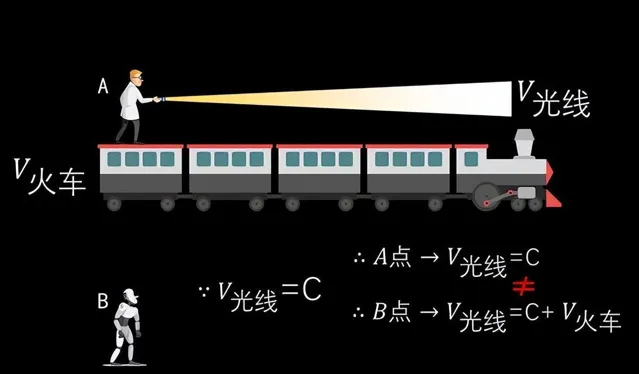
因為速度就等於距離,也就是空間除以時間,既然在任何參照系下光速都恒定不變,那麽空間和時間必須做出相應改變。
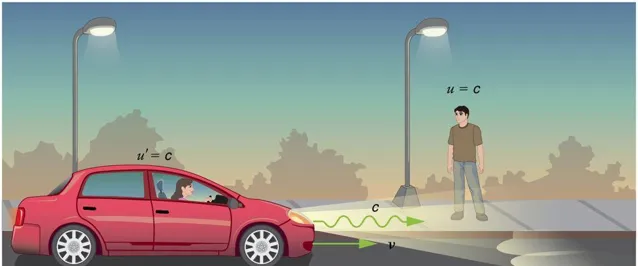
舉個例子,你乘坐一艘飛船,速度為0.5倍光速。我靜止在地面上,手裏拿著手電筒,開啟之後手電筒發出一束光,你乘坐飛船追趕這束光。
這束光在我們眼裏的速度是光速,這很好理解。那麽對於你來講,你看到這束光的速度是多少呢?

你或許會認為,由於你以0.5倍光速追趕這束光,你會看到這束光的速度應該是0.5倍光。事實上並非如此,你相對這束光的速度仍舊是光速。
我們的運動狀態不同,靜止的我和亞光速飛行的你看到一束光的速度是一樣的,那麽必然有某些東西要改變, 不然 我們看到的光速不可能是一樣的。
而速度只與時間和空間有關,所以改變的必然是時間或者空間。而愛因史坦強調,時間和空間是一個整體,所以時間空間必然同時改變。

光速的這種絕對性,也就是光速不變原理明顯違背了我們的直覺,但這個結果完全符合實驗結果,科學家們進行了很多次實驗,結果都表明光速確實是不變的。
這也是愛因史坦之所以大膽假設「光速不變」的主要原因。沒錯,光速不變原理就是一個假設,也可以說是公理,與「兩點之間,線段最短」一樣都是公理。任何公理都無需證明,也沒有辦法完全證明。
當然,愛因史坦並不是隨便就提出「光速不變原理」的。理論上講,既然光速不變是假設,你完全也可以提出自己的假設代替光速不變原理,然後在你的假設的基礎上,建立一套自己的理論,這完全沒有問題。
但前提是你的假設必須符合實驗結果,並且保證你的理論是自洽的。還有一點,假設的東西必須盡可能少,因為任何假設就像一顆「定時炸彈」,隨時可能會引爆。假設的東西越多,出錯的機率就越高!











