「……在各種化學變化中,都不會發生物質損失……在各種物理變化中,都不會發生能量損失。」
——亨利·恩飛·羅斯科爵士
亨利爵士的這段話讓我們想到了一個看似非常簡單的問題:
因為沿途它的波長會擴大,因此它的能量必然會減少。畢竟,如果說我們對能量有什麽認識的話,那就是能量守恒定律:能量既不能被創造,也不能被淪陷。

當你燃燒木頭生火時,你可能會認為你在產生能量。但實際發生的事情要微妙得多:
· 分子鍵被斷裂和重新形成,從不太穩定的結構(木材和氧氣)轉變為更穩定的結構(木灰和水蒸氣),並在這一過程中釋放能量。
· 如果您觀察釋放的能量並使用愛因史坦著名的轉換公式E = mc^2,您實際上會發現產物和反應物分子的品質之間存在微小的品質差異。
· 事實上,包括品質在內的所有形式的能量的總和在反應的每個步驟中都是不變的。
在核反應之類的事情中,品質差異甚至更加明顯,比如在太陽中發生的事件。事實上,如果你測量太陽從誕生到現在的品質,你會發現,在 45 億年的能量釋放過程中,太陽的品質損失大約相當於土星的品質。

但有時,物質似乎會失去能量,而沒有任何東西似乎會獲得能量(或品質)來補償。膨脹的宇宙就是這種情況。愛因史坦廣義相對論帶來的新事物之一是空間本身是可變的,而不是萬物賴以生存的固定座標「網格」。宇宙可以而且必須根據內部物質和能量的數量和配置而彎曲,宇宙的結構也可以膨脹或收縮。
但問題是,任何光子(或光粒子)的能量都由其波長決定。如果宇宙的結構伸展(膨脹時)或收縮時,光的波長(因此其能量)也會發生變化。
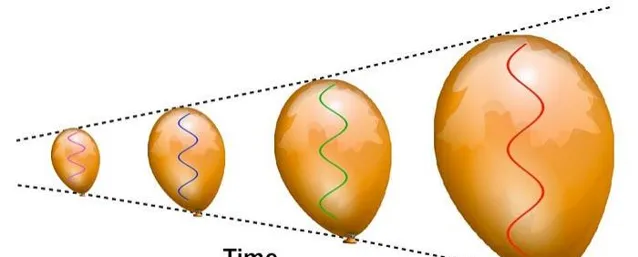
這應該會讓你感到困擾!畢竟,我們認為在宇宙中發生的任何物理過程中,能量都應該守恒。廣義相對論是否可能違反能量守恒定律呢?
答案可能真的是這樣,廣義相對論對許多量都做了出色而精確的定義,但能量卻不是其中之一。換句話說,愛因史坦方程式並沒有規定能量必須守恒;廣義相對論根本沒有定義能量!但這並不意味著我們不能為它給出定義;這只是意味著我們必須小心。
一個很好的類比是瓦斯。當你給瓦斯添加能量(熱量)時會發生什麽?瓦斯中的分子在獲得能量時會移動得更快,這意味著它們的速度會增加,它們會更快地擴散以占據更多的空間。
但是,如果加熱封閉在容器中的瓦斯,會發生什麽情況呢?
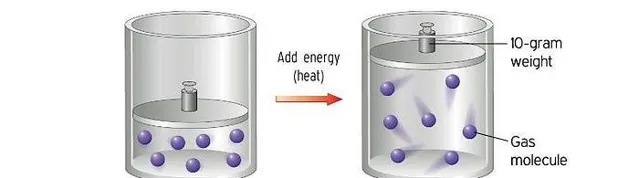
是的,分子會升溫,它們會移動得更快,並試圖散開,但在這種情況下,它們經常會撞到容器壁上,從而在容器壁上產生額外的正壓力。容器壁被向外推,這會消耗能量,也就是說分子正在做功!
這與膨脹宇宙中發生的事情非常相似。光子具有能量,由波長決定,隨著宇宙膨脹,光子的波長被拉長。這當然意味著光子正在損失能量,但宇宙內部所有有壓力的物質都在對宇宙本身做功!
嚴格來說,正如我們之前提到的,廣義相對論中並沒有為宇宙本身定義能量。但如果我們把宇宙本身的結構拿來並使其收縮,它裏面的光子會發生什麽?收縮的宇宙會對光子做功(而不是相反),並使它們獲得能量。
有多少能量?正好與宇宙膨脹時它們所損失的能量一樣多。
所以隨著宇宙的膨脹,光子會失去能量。但這並不意味著能量不守恒;這意味著能量以功的形式進入宇宙空間的膨脹本身。如果宇宙逆轉膨脹並再次收縮,那麽功就會反向完成,並直接回到內部的光子中。
在更完整(即量子)的重力理論中,可能會出現更嚴格的能量定義,我們將能夠真正看到能量是否守恒。但在沒有嚴格定義的情況下,我們所能做的就是利用我們現有的資源,而這些是我們已經擁有的工具和定義來解釋這個問題,並給出答案——是的,光子會損失能量,但這種能量不會永遠消失;能量損失(或增益)的數量加起來恰好等於膨脹(或收縮)宇宙中的能量。











