
數學是純粹理性的象征。科學的很大一部份是以數學和邏輯為基礎的。在某種意義上,數學就是理性的語言,它是所有人類發明中最成功的。然而正如我們即將看到的那樣,就連數學也有自己的局限。

本文節選自【理性的邊界】 第九章 數學面臨的障礙,此書「返樸的書店」有售,有意者可點選小程式搜尋書名購買。
撰文 | [美] 諾桑·亞諾夫斯基
譯者 | 王晨
1 寫完這封信,就去捍衛愛情了
巴黎,1832 年 5 月 29 日。一名年輕的男子正在奮筆疾書。他必須快速寫下這封長信,因為需要寫的內容很多,而他知道自己第二天就會死於非命。
這封信是對他的數學研究的總結,他想在為時太晚之前將這些內容全部寫在紙上。他在信的最後懇求他的朋友:「向 (聞名世界的數學家) 亞可比或高斯征求他們的公開意見,不是讓他們判斷這些定理的真實性,而是評價它們的重要性。我希望將來有人能夠解開這團亂麻。」
第二天,他為了捍衛對一名女子的愛情而參加了一場決鬥,結果正如他所料,他受了致命的重傷。被帶到當地醫院之後,他只活了一天。據說他最後的遺言是說給他哥哥的:「別哭,艾爾弗雷德!我需要我所有的勇氣才能在 20 歲死去。」這個年輕人的名字是埃瓦裏斯特·伽羅瓦 (Évariste Galois,1811—1832) ,而他的工作將永遠是現代數學的重要組成部份。
這封信裏有什麽?20 世紀最偉大的數學家和物理學家之一赫爾曼·外爾寫道:「如果按照它所含資訊的新穎性和深刻性來看,這封信或許是人類所有文獻中最重要的著作。」 或許外爾在做這個評價時有些浮誇了,不過伽羅瓦的研究成果的確包含對現代數學和物理學至關重要的思想。一個 20 歲的年輕人能夠說出什麽重要的理論呢?
伽羅瓦出生於 1811 年,當時法國大革命之後的狂熱氣氛還沒有散去,這讓伽羅瓦度過了短暫而悲劇的一生。他的父親曾經是巴黎郊外一個小城市的市長,後來因為一場激烈的政治爭端而自殺。伽羅瓦是一個滿懷激情且心思復雜的年輕人,他的成長過程很不容易。他很年輕的時候就癡迷於數學,以至於荒廢了其他方面的學習。他沒有考上法國最負盛名的巴黎綜合理工學院 (École Polytechnique) ,最終進入了一所第二梯隊的大學,但老師並沒有真正地發現他的聰明才智。伽羅瓦送出了兩篇用來發表的論文,結果都被編輯弄丟了。後來他參與了激進的政治團體,導致自己被學校開除。目前還不清楚這次致命決鬥的另一方是誰,引起決鬥的女子的身份也未知。如果這位年輕的天才沒有以這麽悲慘的方式英年早逝,他還能完成什麽樣的工作呢?這個問題的答案只能靠猜測了。
伽羅瓦的工作和多項式方程式的求解有關。在理解他的貢獻之前,我們必須先研究一些歷史。思考下面這個簡單的方程式:
ax + b = 0
此類方程式稱為「線性」方程式,大多數中學生知道如何求 x:
x = –b/a
更復雜的「二次」方程式是下面的形式:
ax ^ 2 + bx + c = 0
古典時代的人們就已經知道了這種方程式的求解方法,而且一直到現在,高中學生還在學習使用「二次公式」求二次方程式的解。二次方程式實際上有兩個解:
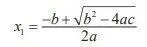
及
註意這些公式使用了加法、減法、乘法、除法、求平方和平方根等運算。那麽「三次」方程式呢?如下所示:
ax ^ 3 + bx ^ 2 + cx + d = 0
這種方程式的求解存在標準公式嗎?16 世紀,傑羅拉莫·卡爾達諾指出這個方程式有三個解,而且給出了相當復雜的公式。這些公式使用了普通的運算方式,包括求平方根和立方根。繼續下去,我們可以試著求解「四次」方程式:
ax ^ 4 + bx ^ 3 + cx ^ 2 + dx + e = 0
洛多維科·費賴瑞 (Lodovico Ferrari,1522-1565) 和尼科洛·豐塔納·塔爾塔利亞 (Niccolò Fontana Tartaglia,1499-1557) 發現了四次方程式的解。你一定很想知道我們是否會寫下這四個可能的解對應的四個公式。與其將它們寫下來,不如說這些「四次公式」使用了普通的運算,包括求平方根、立方根和四次方根。那麽「五次」方程式呢?如下如示:
ax ^ 5 + bx ^ 4 + cx ^ 3 + dx ^ 2 + ex + f = 0
事情在這裏變得更有趣了。也許有人會覺得存在由加減乘除和從平方根到五次方根組成的「五次公式」。這是不對的!不存在這樣的公式。19 世紀初,保羅·魯菲尼 (Paolo Ruffini,1765-1822) 和尼爾斯·亨利克·阿貝爾 (Niels Henrik Abel,1802-1829) 證明了不存在這種使用普通運算和求方根的普適公式。這意味著對於每個由a、b、c、d、e、f組成的五次方程式,永遠都不會存在簡單的求解公式。這是數學局限性的又一個清晰的例子。一般而言,這個問題是不可解的。然而某些五次方程式存在很容易找到的解。例如,x5 – 1 = 0 有一個解為 x = 1。
這就是伽羅瓦的工作重心。他能夠使用某個給定五次方程式的系數確定該方程式能否用普通運算求解。為此,伽羅瓦引入了群 (group) 的概念。群是一種以對稱概念為模型的數學結構。伽羅瓦指出了如何將一個群與每個方程式關聯起來。在這些對稱性的幫助下,他能夠判斷某給定五次方程式能否用普通運算求解。當他對五次方程式求解的工作得到理解之後,就立即被用在數學和科學的許多其他領域。
這種描述對稱性的概念涉及現代數學、化學和物理學的一次重大革命。現代數學和科學的很大一部份研究的是不同形式的對稱性,因此也就是不同型別的群。從這個角度,我們終於可以理解外爾對伽羅瓦書信內容積比重要性的判斷:現代數學和科學廣泛地使用了伽羅瓦引入的觀念。
如果要一五一十地介紹伽羅瓦理論 (Galois theory) 究竟是如何發揮作用的,我們一定會暈頭轉向。簡要地介紹一下就足夠了,這個理論首先描述了數學或物理系統的對稱性。建立了這種對稱性之後,研究人員就要確保這種對稱性在不同運算或物理法則下得到保持。一個系統不能違反自身的對稱性,這個事實可以看作對該系統的限制。
我們在 9.1 節見到的不可解決的古典尺規作圖問題都可以使用伽羅瓦理論證明其不可解決。我們還沒有討論的另外一個問題是某些正多邊形 (regular polygon) 是否可以用尺規作圖構造。等邊三角形和正方形是可構造的。正五邊形呢?任意的正 n 邊形呢?伽羅瓦理論告訴我們哪些正 n 邊形可以使用尺規作圖構造出來。所以如果
n = 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, …, 257, … , 65 537, …
那麽與之相應的正 n 邊形就是可構造的。相比之下,如果
n = 7, 9, 11, 13, 14, 18, 19, 21, 22, 23, 25, …
那麽這樣的正 n 邊形就是不可構造的。
伽羅瓦理論描述的這種限制性體現在一個很有趣的例子上,那就是經典的兒童遊戲十五子棋。這個著名的益智遊戲有 15 個小方塊安裝在一個 4×4 的網格裏。每次可以移動一個方塊,目標是讓這些方塊按順序排列,如圖 9-6 的右半部份所示。然而某些開局排列方式無法得到按順序的排列方式。只要簡單地交換一下編號為 14 和 15 的方塊的位置,就無法得到按順序的排列方式,也無法從按順序的排列方式恢復到最初的排列方式。
實際上這些方塊可能的排列方式一共有 15 的階乘 (15!) 種。這些方式中正好有一半稱為「偶排列」 (even permutation) ,而另一半稱為「奇排列」 (odd permutation) 。方塊普通形式的移動有一種對稱性,只能從偶排列變成偶排列,或從奇排列變成奇排列。這些現象體現了該系統的對稱性。在圖 9-6 中,一種排列方式是偶排列,而另一種是奇排列。
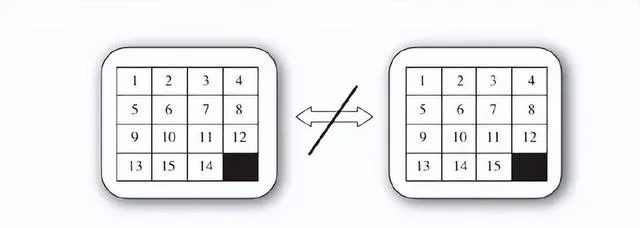
正是因為這個事實,所以無論我們進行多少次規則範圍內的移動,都無法將一種排列方式變成另一種。
還可以在魔術方塊上看出與伽羅瓦理論有關的不可能性。拿出一個完全拼好的魔術方塊,然後只扭動它的一個角 (盡管這違反規則) 。將它打亂,然後讓一個觀察力不佳的朋友 (沒看過本書的朋友) 試著拼回原狀。這是不可能完成的。一次扭動就讓它無法恢復原狀,無論用多少步驟也不行。
總之,伽羅瓦的方程式理論指出了乘法、除法、乘方和求方根等普通運算在方程式求解中固有的局限性。多年以來,數學家開發出了使用微積分和無窮方法的其他技術,解決了這些問題的一部份。所以伽羅瓦理論證明了某些問題無法用特定方式解決。與之類似,如果允許使用直尺測量確切的長度,那麽所有正 n 邊形都可以構造出來。對於十五子棋遊戲,只要將所有棋子都拿出來,再按照正確的順序擺回去就很容易解決問題。透過作弊的方式總能解決魔術方塊問題,也就是將它一塊塊拆開,再按順序拼裝起來。這些都是繞過伽羅瓦描述的數學局限的簡單招式。
2 電腦永遠無法解決的判定問題
假設你找到了一份工作,是在某個建築承包商手下打工,幫助客戶設計他們夢想中的廚房。本來一切順利,直到某個百萬富翁的妻子走進來,想更換廚房的地板。她不想要樣式普通的方磚,而想別出心裁地使用圓形的磚。你向她指出圓形的磚沒法用,因為會留下無法填充的縫隙,如圖 9-7 所示。
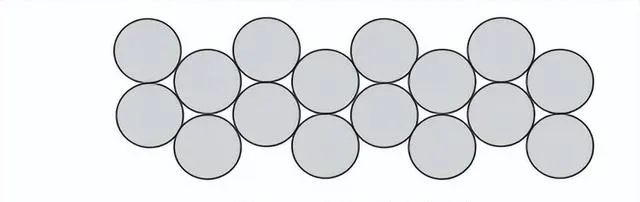
正五邊形適合嗎 (見圖 9-8) ?
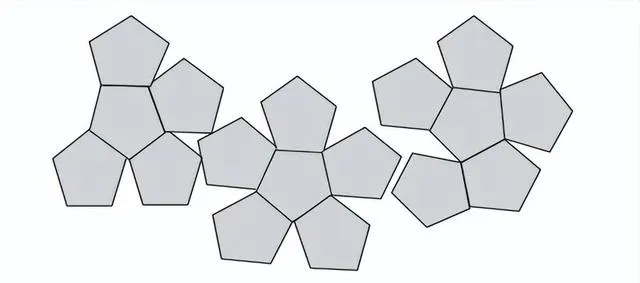
正五邊形也不適合,但你沒有放棄,又向她提議使用正六邊形,如圖9-9 所示。
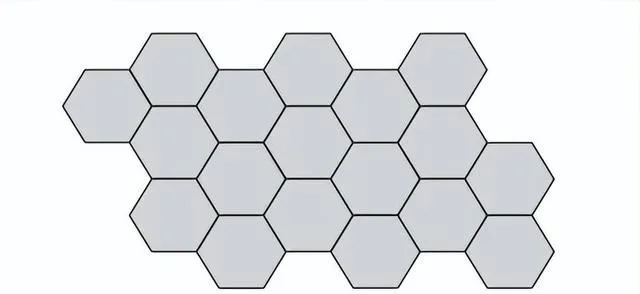
這次沒有空隙了。正六邊形可以用來給地板拼磚。可以看出,有些形狀適合無縫拼接,有些形狀不適合。圖 9-10 展示了其他兩種只使用一種形狀的拼接方法。

很顯然還有許多其他形狀可以嚴絲合縫地拼接起來。聞名世界的荷蘭畫家M. C. 埃舍爾 (M. C. Escher,1898-1972) 制作了一些精彩的蝕刻版畫,他將這些奇怪的形狀彼此拼接在一起,不留一丁點兒縫隙。
思考圖 9-11 中稱為邁斯圖形 (Myers shape) 的怪異形狀。
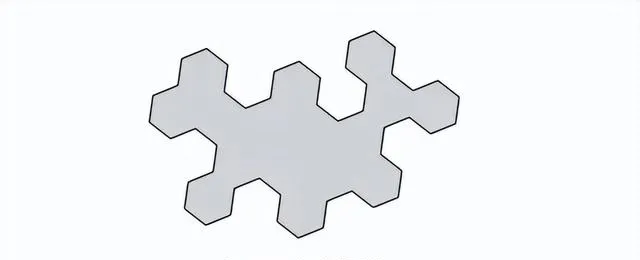
有人也許會覺得形狀如此奇怪的拼塊不可能不留縫隙地覆蓋地板。但是它完全可以做到這一點。如圖 9-12 所示,一點兒問題也沒有。

我們見到的大多數形狀在拼接時使用的方法會讓拼接出來的圖案自我重復。這種拼接方式被稱為具有周期性。在周期性拼接中,同樣的圖案一次又一次地出現。然而某些形狀擁有不存在重復圖案的拼接方式。這種拼接方式被稱為具有非周期性。思考長寬比為 2×1 的矩形。這個形狀很容易創造周期性拼接。
然而我們也可以用這種矩形創造非周期性拼接。將兩個這樣的矩形拼在一起就得到了一個正方形,這種正方形可以垂直或水平放置,如圖 9-13 所示。由於任何圖案都可以像這樣創造出來,因此創造非周期性拼接很容易。
我們還可以在非周期性圖案的問題上向前再走一步。存在某些形狀的組合,當你用它們來拼接時,它們形成的圖案永遠不會是周期性的。換句話說,這些形狀只能拼接出非周期性圖案。因此,這些形狀被稱為非周期性拼塊。羅傑·潘洛斯 (Roger Penrose) 發現了兩組這樣的形狀,其中一組是「風箏」和「飛鏢」,另一組叫作菱形 (見圖 9-14) 。
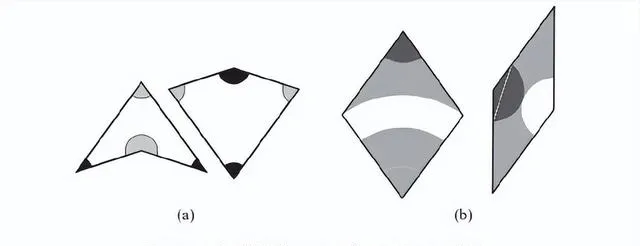
這些形狀有不同的顏色。當這些形狀的拼接方式令相同的顏色對接在一起時,形成的圖案就不會是周期性的。圖 9-15 和圖 9-16 就是這種非周期性拼接的例子。
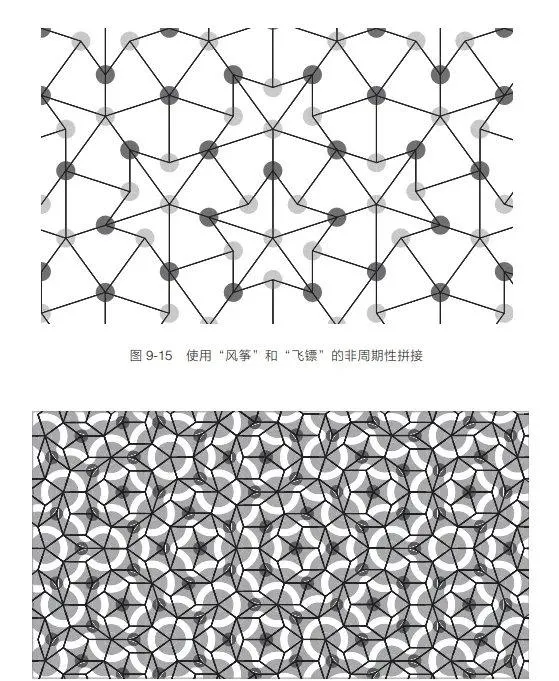
讓我們回到幫別人拼廚房地板磚的工作上。如果存在某種方式能將不同形狀的組合輸入一台電腦,讓它告訴我們這些形狀能否拼接成一塊沒有縫隙的大地板 (不用考慮邊緣問題) ,那就太妙了。我們將這個接受形狀並判斷它們是否適合拼接的任務稱為拼接問題 (tiling problem) 。能夠解決拼接問題的電腦會對圓形和正五邊形回答「否」,對正方形、等邊三角形、正六邊形、邁斯圖形、潘洛斯的「風箏」和「飛鏢」以及潘洛斯的菱形回答「是」。這樣的電腦程式對你的工作會有巨大的幫助。
可惜的是,這樣的電腦程式不可能存在。20 世紀 60 年代中期,勞勃·伯傑 (Robert Berger) 證明了不存在能夠解決拼接問題的電腦程式。
他證明這一點的方法是指出這個問題比我們在第 6 章見到的停機問題還難。停機問題問的是某個電腦程式是最終停機還是陷入死迴圈。如我們所見,任何電腦都不可能解決停機問題。既然拼接問題更難,那麽它也不能被任何電腦解決。
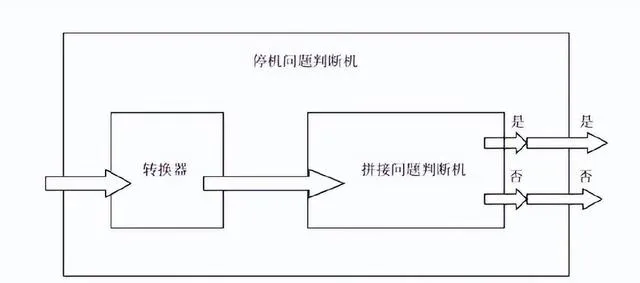
具體地說,可以將任何計算過程轉換為一組形狀,並使得若且唯若這些計算過程永不停機的時候,這些形狀才能拼接出一個平面。也就是說這些形狀能夠拼接地板被等同於計算過程進入死迴圈。 (我們在 6.3 節中見過這種轉換過程。) 可以用圖 9-17 形象化地表示這種一個問題轉換 (或歸約) 為另一個問題的過程。
在這幅示意圖中,一個程式從左側進入,然後轉換成一組形狀。假設 (錯誤地) 存在一台電腦可以判斷一組形狀能否形成無縫拼接。那麽我們就擁有一種方法可以判斷某個程式是陷入死迴圈還是停機。由於我們已經知道沒有任何方法能解決停機問題,因此我們就知道沒有任何方法能解決拼接問題。
像拼接問題這樣電腦永遠無法解決的判定問題叫作不可判定問題 (undecidable problem) 。雖然這些問題有清晰的定義和客觀存在的答案,但任何電腦永遠都無法解決它們。
值得強調的是,我們證明拼接問題不可判定的方法是基於停機問題不可判定這個事實的。
停機問題可判定矛盾。
圖 9-17 指出:
拼接問題可判定停機問題可判定。
將這兩個蘊涵推導結合起來,我們得到拼接問題可判定矛盾。因此拼接問題不可判定。判斷一組特定的形狀能否用來拼接地板,這只是比停機問題難因而不可判定的眾多問題之一,這樣的問題還有很多很多。
本文經授權轉載自微信公眾號「圖靈新知」。
特 別 提 示
1. 進入『返樸』微信公眾號底部選單「精品專欄「,可查閱不同主題系列科普文章。
2. 『返樸』提供按月檢索文章功能。關註公眾號,回復四位陣列成的年份+月份,如「1903」,可獲取2019年3月的文章索引,以此類推。











