古時候,陶瓷的生產是沒有什麽理論指導的,完全依靠工人師傅們長期的經驗積累。直到上世紀三、四十年代以後,人們才在現代物理、化學知識的基礎上,逐漸發展出各種科學、理性的燒結理論,用於指導陶瓷的制備和生產。雖然到目前為止,陶瓷燒結理論還遠遠談不上完善成熟,但在多數情況下,用於定性地解釋燒結現象、分析背後的原因還是比較靠譜的。
不過,相對於解釋和分析,如今的燒結理論在預測方面卻顯得比較差強人意。比如吧,我們可以透過一組實驗,可以擬合出一條陶瓷的燒結曲線(密度-溫度曲線或密度-時間曲線),然後可以根據這條曲線對粉體不同溫度下的致密化行為做一些簡單的分析。但是,如果你以為有了這條燒結曲線就可以對該種粉體的燒結行為做出多麽準確的預測的話,那可能就是想多了。原因也很簡單,燒結曲線受各種因素的影響,比如升溫速度不相同的話,燒結曲線大機率也會不一樣。
那麽,有沒有什麽燒結曲線可以更準確地預測粉體的燒結行為呢?
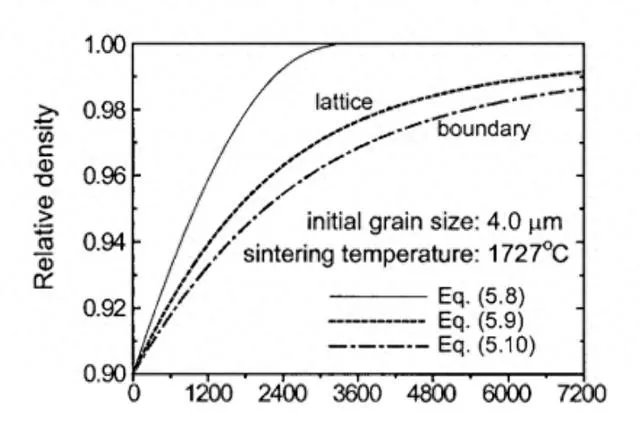
還真有,就是所謂的主燒結曲線。主燒結曲線與熱處理的路徑無關,從而提供了一種簡便的預測燒結行為和致密化的方法。
那這個主燒結曲線又是怎麽回事呢?
原來,這是基於一種新型的燒結理論推匯出來的一種燒結曲線。我們所熟知的很多燒結理論,都存在一個相同的缺點,就是它們都往往是根據某一單一燒結機制或針對某一燒結階段所提出來的,不同的燒結階段,燒結機制、燒結模型都可能不同。因此根據那些燒結理論預測的陶瓷燒結行為往往與實際情況相差很大。而主燒結曲線的基礎,則是一種由Hassen等人在1992年提出來的被稱為全期燒結模型的新型理論。1996年,Su等人等根據全期燒結模型,從致密化速率的公式推匯出主燒結曲線理論。該理論將致密化速率方程式式以變量分離的方法分解成與顯微結構及與燒結制度相關的兩部份,分別放在方程式式的兩邊,從而使燒結過程的預測成為可能。主燒結曲線理論推出的時候,並沒有引起太大的註意,但進入21世紀後,其受到的關註度卻越來越高,實用價值不斷得到認可,套用越來越廣泛。
主燒結曲線一般呈 S 型,其座標軸與普通的燒結曲線有所不同,其縱軸為相對密度,橫軸卻不是溫度或時間,而是一個 θ 值,這個 θ 值是溫度和時間的函式。因此,主燒結曲線實際上是涉及時間、溫度和相對密度3個變量的特殊2 D 曲線。也就是說,透過一條曲線,就可表示出燒結體在不同溫度、不同時間下的致密度。

要建立主燒結曲線,需要知道坯體的相對密度和 θ 值。前者可以由坯體燒結的收縮曲線獲得,而後者則要致密化啟用值來計算。但這個啟用值不知道也無所謂,可以先給出一個值,從而建立兩種升溫速率下的主燒結曲線。然後根據曲線的所有數據點在擬合時產生平均殘留誤差平方來判斷給出的啟用值是否正確。殘留誤差平方值越小,說明擬合優度越高。反之,則需要重新給定啟用值,重復上述擬合過程,直到平均殘留誤差平方足夠地小。建立一系列啟用能值與相應平均殘留誤差平方的關系曲線,曲線中最低點就是接近真實的表觀啟用能。而根據這個表觀啟用能所計算得到的相對密度- θ 值曲線,就是主燒結曲線。該曲線只與粉體的粒度以及素坯的密度有關,而與燒結過程無關。也就是說,只要某種陶瓷粉體顆粒大小和素坯密度確定,其主燒結曲線就可確定。因此,我們可以根據這條曲線,預測陶瓷在不同條件下的致密化過程。
當然,以上說的只是一種理想的狀態。實際上主燒結曲線也還存在一些局限性。因為該理論依然是在一系列基本假設的基礎上建立起來的,比如各向同性收縮、燒結過程只有擴散機制主導等等。這些假設並不總是與事實相符,因此準確度有時候也並不太令人滿意。但無論如何,這也算是人們走向對燒結過程進行定量預測的重要一步吧。











