如何數出「無窮大」？

2024-01-08科學

作者 | [美]喬治·伽莫夫

轉譯 | 吳先先

來源 | 節選自【數學知道一切的答案：從一到無窮大】，民主與建設出版社，2021年6月。

上一節中我們討論了數位，其中有不少都是相當大的數。不過，即便是大到不可思議，就像西薩·班·達依爾要求的麥粒數目那麽大，這些數位仍然是有限的。只要給足時間，人們就可以把這些數位從頭到尾寫下來。

不過，還有一些具有無窮性的數，無論花多少時間都寫不完。例如，「所有整數的數量」顯然是無窮大的，「一條線上所有幾何點的個數」亦是如此。對於這樣的數，我們除了說它們是無窮大的以外，還可以嘗試其他的描述嗎？換句話說，有沒有可能比較兩個不同的無窮數，看看哪一個「更大」？

「所有整數的個數和一條線上所有幾何點的個數相比，哪一個更大」——這樣的問題有意義嗎？著名的數學家格奧爾格·康托爾（Georg Cantor）最先考察了這個乍看上去有點天馬行空的問題，他是「無窮數學」當之無愧的開創者。

想要談論無窮數的大小，就會有一個問題隨之而來：我們既沒法表示這些數位，也無法把它們寫下來。這就有點兒像一個正在清點自己百寶箱的霍屯督人，他想知道自己手裏的玻璃珠子多，還是銅幣更多。相信你還記得，霍屯督人無法數出 3 以上的數位，那麽，他會不會因為數不出珠子和銅幣各自的數量，就放棄比較這兩個數的大小呢？不一定。如果他足夠聰明，就會把珠子和銅幣逐一比較直至得出答案：把一顆珠子擺在一枚銅幣邊上，另一顆珠子擺在另一枚銅幣邊上，就這樣擺下去。如果珠子用完了，銅幣還剩下幾枚，他就會知道，銅幣比珠子更多；如果銅幣用完了，還有幾顆珠子，那麽就是珠子比銅幣多；如果兩者同時用完，那就是一樣多。

康托爾在比較無窮數時，用的也是完全相同的辦法：把兩組無窮數進行配對，如果這兩個集合裏的每一個元素都能一一對應，最後沒有任何元素剩下，那麽這兩組無窮數就是相等的；如果其中一個集合裏的有元素無法配對，那麽就可以說，這組無窮數要比另一組更大一些，或者說更強一些。

這個方法無疑是可行的，事實上，要比較無窮大的數位，也只有這個法子了。不過，在真正開始采用這個方法之前，我們得做好大吃一驚的心理準備。比如說，我們來比較一下所有的奇數和偶數這兩個無窮數集合。從直覺上判斷，你肯定會覺得奇數和偶數一樣多，而且它們也完全符合上述的規則，二者可以做到一一對應：

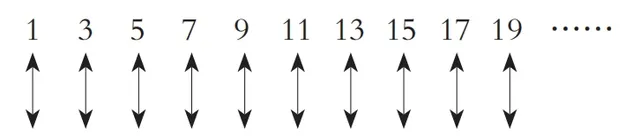
在這個表裏，每一個奇數都對應著一個偶數，反之亦然。因此，奇數和偶數是大小相等的無窮數。看上去很簡單，也很自然！

不過，稍等一下。下面這兩個數，你覺得哪個更大：所有整數的數量（包括所有的奇數和偶數），還是所有偶數的數量？你當然會選擇前者，因為它既包括了全部的偶數，也包括了全部的奇數。但這只是你的直覺而已。想要得到準確的答案，就必須套用無窮數比較的規則。如果你真的這麽做了，就會吃驚地發現自己的直覺是錯的。實際上，所有的整數和所有的偶數也可以放在如下這個表中，實作一一對應：

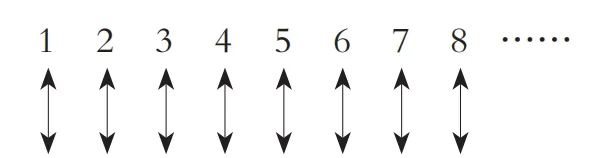
依照無窮數比較的規則，我們只能得出如下結論： 所有的偶數和所有的整數 個數完全相等。 當然，這聽起來有點自相矛盾，因為偶數只是整數的一部份，但是必須要記住，我們在這裏計算的是無窮數，它們的性質會不太一樣。

沒錯， 在無窮數的世界裏，部份確實有可能等於整體！ 最好的一個例證，莫過於德國數學家大衛·希爾伯特（David Hilbert）講的一個故事。他在課堂上的這段話描述了無窮數的矛盾內容 ^[1] ：

「我們來想象一個旅館，它的房間數量是有限的，而且所有房間都住滿了人。假如有一個新客要求入住，那麽老板會說：‘抱歉，所有房間都住滿了。’再來想象另一家旅館，這裏有無窮個房間，同樣，每一個房間裏都住上了人。這時又有新客來訪，要求入住。

「‘沒問題！’旅館老板會立刻答應下來，並把之前住在一號房的客人移到二號房，二號房的客人移到三號房，三號房的客人移到四號房，依此類推……這樣，新客就可以住進調整後空置出來的一號房裏了。

「我們再換個方式，想象一個同樣有無窮多個房間的旅館。所有的房間都客滿，並且有無窮多個新客要求入住。

「‘好的，先生們，請稍等。’旅館老板說道。

「緊接著，老板把一號房的客人移到二號房，二號房的客人移到四號房，三號房的客人移到六號房……以此調整。

「現在，所有門牌號是奇數的房間全都空置了，無窮多個新客人就可以輕松入住進去了。」

希爾伯特描述的這個場景可能不太容易想象，畢竟現在不是戰時的華盛頓，沒有那麽多要住店的客人。不過這個例子很好地說明了在進行無窮數的運算時，我們會遇到一些和普通算術不太一樣的運算內容。

依據康托爾的無窮數比較規則，我們還可以證明，所有分數（如 ,

）和所有整數的個數是相等的。我們可以按照如下的規則，把所有分數排成一排：先寫出分子和分母之和等於 2 的分數，這樣的分數只有一個，即；再寫出分子和分母之和等於 3 的分數，即和；接下來是分子和分母加起來等於 4 的分數，包括和、和 ……，以此類推。按照這個步驟，我們會得到一個包含了所有分數的無限數列（圖 5）。現在，在這個數列旁邊寫出整數的數列，就可以實作無窮多個分數和無窮多個整數的一一對應。所以說，它們的數量是相等的！

你可能會說：「聽上去不錯。不過，這不就意味著，所有的無窮數都是一樣大的嗎？如果是這樣，比較它們的大小還有什麽意義呢？」

不，事情當然沒有那麽簡單。人們可以很容易地找出比所有的整數或分數的個數還要大的無窮數。

現在回過頭來，研究一下本章開頭提出的問題。「一條線上所有點的個數」和「所有整數的個數」，到底誰大誰小？你會發現，這兩個無窮數的大小確實是不同的——一條線上的點的個數要比所有的整數或分數個數要多得多。為了證明這一點，我們試著在一條線段上（比如說 1 英寸長），建立點和整數數列之間的一一對應關系。

線段上的每一個點都可以表示為它與線段某端間的距離，而且這段距離都可以記作一個無限小數，比如 0.7350624780056……，或 0.38250375632…… ^[2] 。現在我們就可以來比較所有整數和這些無限小數的個數了。那麽，上面這些無限小數，和像、

這樣的分數，又有怎樣的區別呢？

大家一定還記得，我們在數學課上學過，每一個普通分數都可以轉化成無限迴圈小數，比如

我們上面已經證明過，所有普通分數的個數和所有整數的個數是相同的，因此，所有迴圈小數的個數和所有整數的個數也是相同的。但是，一條線段上的點不可能完全表示成無限迴圈小數，而且大多數情況下，這些無限小數是不迴圈的。很容易看出來，在這種情況下，兩個數列無法建立一一對應的關系。

假如有人聲稱，他能建立如下形式的對應關系：

當然，因為我們不可能寫出無限不迴圈小數的每一位數，所以這張表的作者必定已經找到了某種一般性的規則（類似於我們將分數和所有整數進行配對的規則），並且按照這種規則構造了上面這個表，這種規則確保，我們所能想到的任何一個小數遲早都會出現在這張表裏。

然而，不難證明，沒有一種排列法則可以保證這樣的事，因為我們總是可以寫出一個沒有出現在這個表裏的無限不迴圈小數。如何辦到的？再簡單不過了只要讓這個數的小數點後第一位數位和表裏的一號數位（N1）的小數點後第一位不同，第二位數位和 N2 的小數點後第二位不同，依此類推，就會得到一個類似下面這樣的數位：

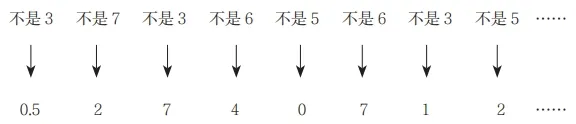
這樣的話，無論你往下找多久，這個數位都不會出現在這個表裏。如果這張表的作者告訴你，你寫下的這個小數就在第 137 行（也可以是其他任意一行），那麽你可以立刻告訴他：「不可能，因為這兩個數在小數點後第 137 位上的數位是不同的。」

因此，一條線上的點的個數和整數的個數之間，無法建立一一對應的關系，這意味著， 一條線上的點的個數比所有整數或分數的個數更大，或者說更強。

我們一直在討論「1 英寸長的線段」上點的個數，不過，根據「無窮數學」規則，很容易證明上述結論對任何一條線段上的點都適用，也就是說， 無論是 1 英寸、1 英尺，還是 1 英裏，這些線段擁有的點的數目都是相等的 。想要證明這一點，只要看一下圖 6 就可以。圖上比較了兩條長度不相等的線段 AB 和 AC 上的點的個數。為了在兩條線之間建立一一對應的關系，我們從 AB 上的每一點出發，做一條平行於 BC 的線，並將它與兩條線的交點進行配對，例如 D 和 D1、E和 E1、F 和 F1 等。如此一來，AB 上的每一個點在 AC 上都有點與之對應，反之亦然。因此，根據我們的規則，這兩條線段擁有的點的數量是相等的。

在探索無窮大數的過程中，我們還有一個出人意料的發現： 一個平面上的所有點的數量和直線上點的數量竟然是一樣的！ 為了論證這一點，我們來考察線段 AB（長度為 1 英寸）上面的點，和正方形 CDEF 內的點（圖 7）。假設線段 AB某個位置上的點均可以用某數位來表示，比如說 0.75120386……，那麽，我們可以由這個數位確定兩個不同的數位，取小數點後的奇數位和偶數位重新組合，即0.7108……和 0.5236……。

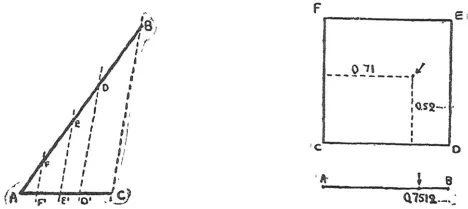
接下來，我們分別以這兩個數位為橫座標和縱座標的值，在正方形中尋找到對應的點，並把這個點稱為此前線段上點的「對應點」。反過來，如果我們知道正方形裏任何一個點的橫座標和縱座標，打個比方，比如說 0.4835……和 0.9907……，透過相同的規則合並這兩個數位，也可以得到它的「對應點」線上段上的位置：0.49893057……。

很顯然，透過上述的步驟，兩組點之間建立起了一一對應的關系。線上的每一個點都能在正方形裏找到它的對應點，而正方形裏的每一個點也能線上上找到對應。沒有任何一個點會被遺漏。依照康托爾的規則，我們可以得出結論：正方形裏所有點的數量等於線段上的所有點的數量。

使用類似的方法，也很容易證明，立方體內所有點的數量等於正方形或直線上點的數量。我們只需要把原來的小數拆分成三個新的數位 ^[3] ，然後用這三個數來定義立方體內「對應點」的位置即可。此外，就像兩條長度不同的線段中，點的數量是相等的一樣，無論正方形或立方體的大小如何，其中點的數量也不會改變。

雖然所有幾何點的數量比所有整數或分數的數量要大，但它還不是數學家們已知的最大的無窮數。事實上，人們發現， 所有曲線的種類，包括那些最不同尋常的曲線，要比所有幾何點的數量還要多，因此，必須要用無窮數列的第三個數來描述它。

根據「無窮數學」的開創者格奧爾格·康托爾的定義，無窮數可以用希伯來字母 ℵ （aleph）表示，其右下角有一個數位，表示它在無窮數列中的位置。由此，我們可以得到一個數位的序列（其中也包括無窮大數）：

1,2,3,4,5…… ℵ ₀ , ℵ , ℵ , ℵ ……

當我們說「一條線上有 ℵ 個點」，或「存在 ℵ 條不同的曲線」時，就和我們在說「世界分為七大洲」或「一盒紙牌有 52 張牌」時，沒什麽兩樣。

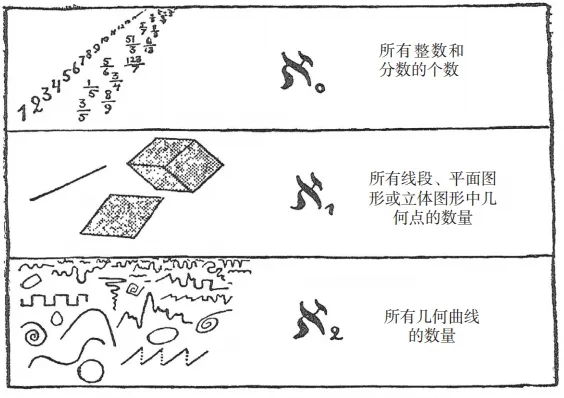
在結束有關無窮數的討論之前，我們需要指出，雖然這些無窮數只分了幾級，但是卻包含了我們能想到的所有無窮大數。我們知道, ℵ ₀ 代表所有整數的個數， ℵ 代表所有幾何點的數量， ℵ 代表所有曲線的數量，但是迄今為止，還沒有人能夠想出用來描述 ℵ 的集合。看來，前三個無窮大數就足以囊括我們所能想到的任何數位，這和我們的老朋友霍屯督人的處境剛好相反：他們明明擁有很多孩子，卻最多只能數出三個！

註釋：

[1] 這段內容從未正式發表過，希爾伯特甚至沒有將它寫成文字，但它流傳甚廣。引自 R. 柯朗，【大衛 · 希爾伯特軼事全集】。

[2]因為我們假定線段的長度是 1，所以這些小數全都比1小

[3]比如 0.735106822548312……這個數我們可以拆分為 0.71853……、0.30241……和 0.56282……。