套用相圖的振動系統的定性分析方法
所謂 振動 ,即物體在一定位置附近做來回往復的運動。 單自由度 的振動系統都可看成是 振子 ,其中最簡單的例子就是 彈簧-品質系統 ,由一個忽略品質的彈簧和一個忽略體積的質點組成。其中質點作為振動的主體,彈簧提供振子的 恢復力 。
圖中D代表彈簧彈性系數K,s0代表彈簧連線質點後的平衡伸長量,s代表質點相對於平衡位置的位移。
在物理課中,我們通常使用牛頓力學的方式建立運動方程式,解出系統位移隨時間變化的運動方程式,以直觀地觀察系統的運動狀態。如之前提到的彈簧振子中,其彈簧恢復力與質點相對於彈簧平衡點的位移x的關系由 虎克定律 指出:在彈性限度內,彈簧的彈性力F的大小和彈簧長度的變化x成正比:
結合 牛頓第二定律 ,彈簧的作用力F與質點的加速度a成正比:
則可以得出彈簧振子的運動方程式:
由於正弦函式和余弦函式的二階導數都是其本身乘以一個系數:

所以可以將這兩個函式的線性組合設為運動方程式的解:
帶入運動方程式可以得到:

由於質點振動時位移x不恒為0,所以:
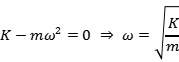
其中ω稱為系統的 固有頻率 ,是由質點的品質m和彈簧的彈性系數K,這兩個物理內容唯一確定的,不隨外界條件而改變。
再利用三角函式中的輔助角公式,我們可以將運動方程式的解寫為正弦函式的形式:

所以我們可以清晰地看出,彈簧-品質系統的振動曲線是一條正弦曲線,這種按正弦規律進行的往復振動稱為 簡諧振動 ,是最常見的振動形式。
至此,我們得到了彈簧-品質系統振動的直觀表現形式,但方程式的解中還有兩個系數C1,C2沒有確定,當這兩個系數確定時,系統的振動方程式也便唯一確定。為了確定這兩個系數,我們需要知道系統在t=0時刻的初始條件:
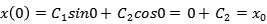
這個式子表明,質點的初始位移x0可以確定系數C2。為了確定C1,考慮到sin0=0和cos0=1,對x求一階導即可將C2部份同上式一樣變為0,即:
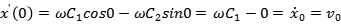
這個式子表明,質點的初始速度v0,可以確定系數C1。所以我們所需要的確定振子運動狀態的兩個量為質點的初始位移和初始速度(x0,v0)。對此加以推廣可以知道,不只有0時刻的位移和速度可以確定兩個系數,任意時刻t的質點位移和速度,都可以確定振子的運動狀態。所以,質點的位移和速度是表達振子運動狀態的兩個變量,稱為 狀態變量 。
現在,我們得到了一組與傳統的直觀表示運動狀態的(x,t)變量不同的新變量組(x,v)。若以x和v為直角座標建立(x,v)平面,則稱此平面為系統的 相平面 。在每個確定的時刻,質點有其唯一確定的位移x和速度v,這與相平面上的點一一對應,這些點稱為 相點 。隨著時間的推移,這些相點構成一條曲線,稱為 相軌跡 。
相平面的原點是一個特殊的點,其表示質點的位移和速度都為0,所以其靜止不動,對應系統的平衡狀態。因此相圖的原點也稱為 平衡點 。因此,當彈簧-品質系統處於平衡狀態靜止時,其對應的運動圖為一條直線,而對應的相圖為一個點。
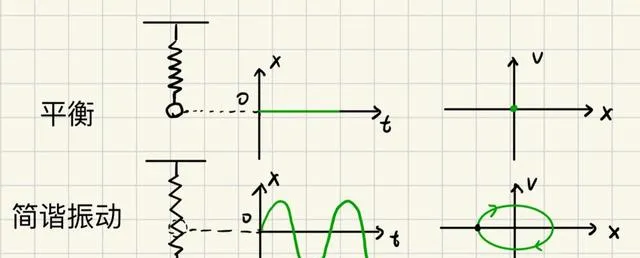
當振子在外界的擾動下開始運動時,相點就離開平衡點位置,改為沿平衡點附近的相軌跡移動。對於簡諧運動,其運動方程式為
則

於是我們可以得到相平面的相軌跡方程式:
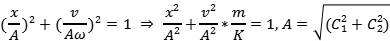
這是一個橢圓方程式,橢圓的大小隨著振幅的增大而增大,相同系統不同振幅的簡諧運動對應的不同橢圓構成一個族,將相平面原點包圍起來,此時相平面原點又可稱為 中心 。這種相圖表示 穩定平衡狀態 附近的振動,如彈簧-品質系統運動的相圖。
既然得到了穩定平衡狀態下單自由度振子的運動相圖,我們自然會思考, 非穩定平衡狀態 下物體運動的相圖又該如何呢?我們可以利用彈簧-品質系統的變體來分析。
在彈簧-品質系統中,質點偏離平衡位置時,恢復力與運動方向相反,使質點回到平衡位置。而非穩定平衡狀態下,質點離開平衡位置後,所受到的力與運動方向相同,使質點更快地離開平衡位置。與彈簧-品質系統相比,相當於將彈簧的彈性系數K變成負值,於是相軌跡方程式將變為:
這是一個雙曲線方程式,因此不穩定的 負剛度 系統對應的相軌跡是雙曲線族,相點只要稍稍偏離平衡點,就會沿著雙曲線越來越快地無限遠去。這種被雙曲線圍繞的原點稱為 鞍點 。
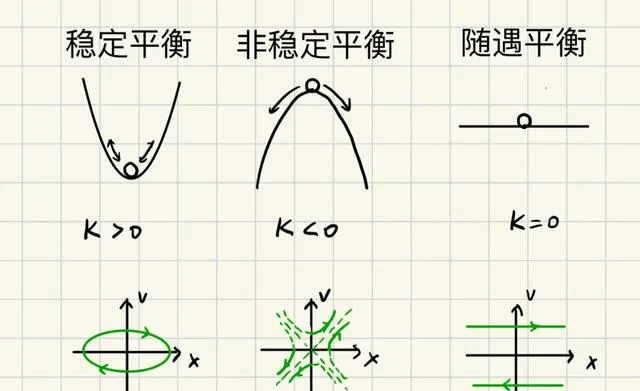
因此,運動的性質可以由相平面原點的型別反映出來,這種利用抽象的相軌跡的幾何特征來判斷實際物體的運動特征的方法,即為振動的定性分析方法。











