二重積分均值定理的幾何意義可以理解為:在特定的有界閉區域上,存在一個點,其函式值乘以該區域的面積等於整個閉區域上函式的二重積分值。
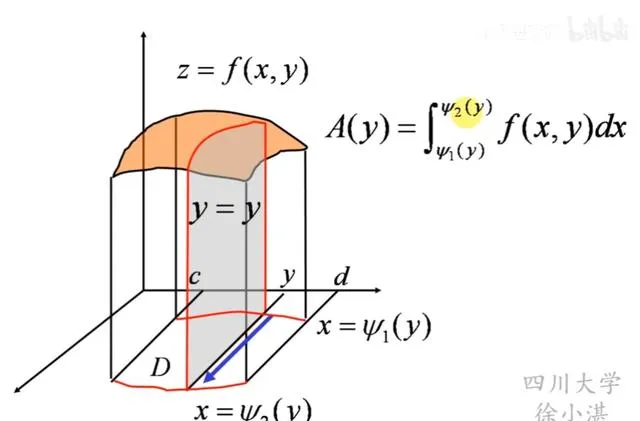
具體來說,這個定理表明,對於一個在閉區域D上連續且有界的函式f(x,y),存在一個點(c,d)屬於D,使得f(c,d)乘以D的面積等於對D進行f(x,y)二重積分的結果。這個定理的幾何意義在於,它將復雜的二重積分問題轉化為了尋找一個特定的點,這個點的函式值能夠代表整個區域上函式的平均水平。
從直觀上講,如果我們想象函式f(x,y)在區域D上的變化類似於一個起伏的地形圖,那麽二重積分均值定理告訴我們,在這個地形中存在一個「平均高度」的點,這個點的高度乘以整個區域的面積,與把整個地形覆蓋一層土壤,使地形完全平坦後的總體積相等。
在套用上,這個定理非常有用,因為它允許我們透過計算一個點的函式值來估計或近似整個區域的積分值,這在解決實際問題時可以大大簡化計算過程。例如,在物理學中,當我們需要估算某個區域的平均溫度或者壓力時,就可以透過找到這樣一個代表性的點來進行測量和計算。











