先致歉:有點兒長,讀完需要點耐心。
已經說過, 我對這次九省聯考試卷的評價一如既往,就是3個字:神經質。當然這個評價相當的主觀,也相當的……咳……不專業。如果要看專業的點評,可以去看章建躍老師對九省聯考數學卷的評析,
「神經質」這三個字從何說起呢?整張試卷除第14,18,19題以外,其余的題目都還算是常規考點,常規考法,總體難度較平,基礎題占了絕大多數,對於中等及以上學生來說題目梯度不夠大,區分度不夠。第18題作為常規的難題,對圓錐曲線的考查比較深入,計算量較大,即使放在最後一題也是夠格的。而第14和19題就屬於命題專家們的放飛自我之作了。14題屬於滿滿的套路+BUG,對於知道套路的學生來說,毫無難度和思維量,而對於不知道套路的學生來說,可能在考場上想破頭也不知道出題人意欲何為。19題就更不用說了,對於競賽生太簡單,對於非競賽生嘛,即使是非常優秀的學生,如果沒接觸過數論,可能也難有頭緒。這種題目放在考試的最後一題,不是廢題是什麽?所以,總體來說,我並不認為這是一份非常好的試卷。最多只能如過去的八省聯考、四省聯考一樣,是一種「試水」。
也正因為如此,所以九省聯考過後,本以為還會像過去那樣一切如常,沒想到很多新高考省份都傳出訊息,今年的高考要采用新的試卷結構,這倒是我事先沒有料想到的。這種訊息一出,必然會引起廣大考生的心中恐慌,甚至開始糾結是否要開始學習數論。那麽,我們面臨這樣的大變革,到底該如何復習備考呢?
首先,我們先來看看試卷結構的對比:
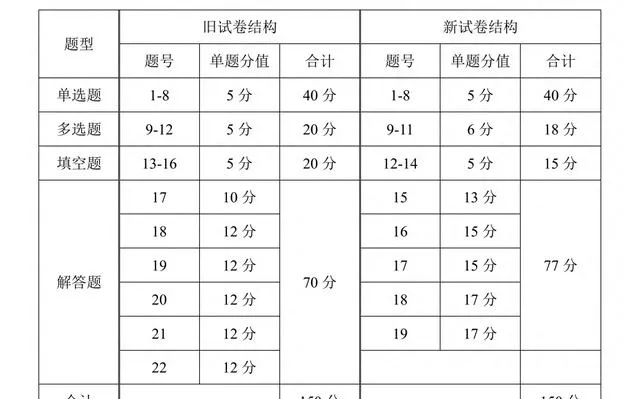
結構上來說,比較明顯的一點在於分值和題量的變化。解答題的題量減少,但總分卻增加了,每一題的分值均高於原來。多選題的題量減少,每一題的分值由原來的5分變成了6分,給分方式也發生了改變:
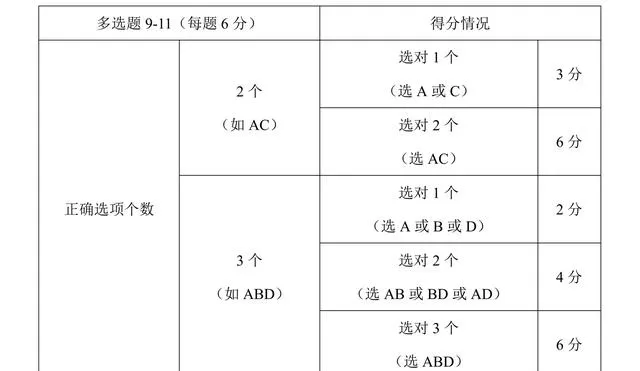
這兩點變化所帶來的最大影響,無疑對於學生的基本功要求更高了,對做題的踏實程度要求更高了。
為什麽這樣說呢?我們先看多選題。過去的多選題,無論正確選項是幾個,少選的總是得2分,全選的得5分,這種給分方式,會導致一種很雞賊的做題方式:中等生,前2個多選題(簡單的),每個選項都看一下,盡量拿5分;後2個多選題(較難的),選一個選項就跑路,反正大多數同層次選手都拿不了5分,何必費那個功夫。而差生則更甚,每個題都選1個,8分到手。反正選不全都一樣,我只要在我同層次的選手中不至於落後,就可以了。而新的給分方式下,只要別人比你多看一個選項,就有可能比你多得至少2分,滿足於過去那種選一個就跑的話,分數可能就沒那麽好看了。這種新的給分方式,顯然更符合新高考加入多選題的初衷:多思考,多辨析,多計算。
至於解答題,數量減少,單題分值增加,一方面,意味著每一題的小問有可能變多,也就是對同一個問題的考查更多面、更深入;另一方面,也可能是增加了過程分,也就是對考生的解題步驟、解題規範要求更高。過去有一些步驟偷懶不寫也許還行,現在可能就會失去相應的分值。尤其是一些證明題,邏輯的嚴謹性要求肯定會更高些。這對於那些懶惰的、不愛好好寫步驟的學生(其中可能不乏一些自己覺得自己天分還不錯的考生)是有很大影響的。
所以,這兩類題目的變化是我們首先要重視的。也是老師在以後的復習備考過程中,要給學生反復強調的。
再從內容上來說。想先說說大家很重視的第19題。講個笑話,九省聯考過後,數論的書一度銷量大增,很多機構開始鼓吹學習奧數的重要性,個人認為很沒有必要。當然這只是個人認為,如果你不這樣認為,那一定是你對,但你對也不妨礙我這樣認為,畢竟每個人都可以有每個人自己的想法,對吧?
之所以這樣認為,是基於以下三點
第一,人家通知只說采用九省聯考的試卷結構,沒說采用它的考試內容。過去每次這種聯考,都會有這種「試水」性質的創新題目出現,比如21年八省聯考那個慘絕人寰的「大興機場」,像「大興機場」這個題目,我也只能說,增加閱讀量以後在高考中會越來越常見,需要閱讀理解的題目會越來越多,但我可沒說以後高考會加進大學裏的什麽曲率之類的東西吧?所以,不能因為這次九省聯考考了一次數論,就認為以後要把數論納入復習範圍。要知道,以前高考考過的每一個新定義題,背後可能都有復雜的背景,那考一次就要多學一門課程,咱們學生還要不要活了,咱們老師還要不要活了?
第二,高考是全國性的考試,並不是所有使用全國卷的地區,學生都有這個資源去接觸那麽多新奇的東西。如果貿然將競賽內容(比如數論)納入高考,那麽一個非競賽生在學習之余自學數論的可能性有多大呢?你們自己想吧。用這種題目來做所謂的「新定義」,對於苦讀三年的廣大學子來說,本身就是一種極大的不公平。尤其是教育落後地區的學生,沒有那麽多資源和渠道去接觸課本以外的知識,遇到這種題目,又當如何?就像2017年全國高考語文作文寫「共享單車」,而很多山區的孩子連共享單車是什麽都不知道。這個題目當年不是引起了軒然大波嗎?
第三,大實話,但可能很殘酷。即使高考真的加入競賽內容,它與絕大多數考生也都是沒有關系的。一個壞訊息是,這些東西不是你學了就一定能會的。當然,還有一個好訊息是,你不會,與你同層次的競爭者大機率也不會,所以,管他加不加呢?與我們何幹?你就當它滿分是133分又如何?當然,有人可能會懟我:你這麽說還不是因為你自己不會!對呀,我是不怎麽會,包括昨天寫解析的時候我也特別指明「我看了答案」。我不會又怎樣呢,不說多的,一般的高考卷子,我還是能做個一百三四十分的吧?連我都不會,你要求多少考生能會?
所以,我認為,與其關註第19題會不會劍走偏鋒,不如關註一下解答題的另一些變化。一個就是我剛才說到的,分值的變化,對我們「寫過程」上提出了新的要求,這裏不再贅述。
另一個是解答題由6道變成了5道,這意味著解三角形和三角函式、數列、立體幾何、機率統計、解析幾何、導數這六大版塊在解答題中又要輪流坐莊了。註意,這裏說的是輪流坐莊,並不意味著某些章節就要結束解答題了(至少目前看不出來,不敢妄言),我們的復習還是要註意全面。別忘了新高考之前的很多年我們也是5個解答題的(選做題另算),那時候也沒有完全刪除這六大版塊中的某一個。當然,也有一種可能就是題目要開始「融合」了,比如,在機率統計題中融入數列、在計算最值的題目(這個三角、機率統計、解析幾何中都有可能)中融入導數等等。既然題量減少了,那就一個題考幾個板塊,這種形式是有可能的,並且在過去的幾次高考中也是有跡可循的。
還有一點是導數位置的提前,這個在23年的高考中早有征兆。與過去導數題牢牢霸榜最後一題(第22題)不同,23年的高考中,導數已經提前到了倒數第四題(第19題)。我不敢保證今後的考試中導數一定都會提前,但總體來說,我覺得高考在弱化導數的壓軸題地位,這是個好事,畢竟這幾年的模擬考中,導數題都太過於妖魔化了,由此也產生了很多不講邏輯只講秒殺的「大佬」,可以說,天下苦導數題久矣。當然,導數題前置的話,對差生不是很友好,除非它真的考得像這次九省聯考一樣這麽簡單,否則,它就依然還是一個坎。











