我們來玩個遊戲...
任意挑選一個正整數。如果它是一個奇數,那麽就乘以3再加1。如果它是一個偶數,那麽就除以2。對得到的新數位做同樣的事,一直這樣做。如果你在某一時刻得出了數位1,那麽就停止。
我知道這可能不是世界上最有趣的遊戲,但請你多玩一會兒。我向你保證,這將是很有趣。
例如,如果我們從7開始,我們會得到下面的數列(從現在開始,我們稱它為科拉茨序列)。
如果我們從19開始,我們得到:
請註意,在某一時刻,我們在上述兩個序列中都得到了數位22,因此它們的「尾巴」是一樣的。
問題是: 我們總是在1處結束嗎?
信不信由你,上述問題是一個深奧的謎題。盡管很多非常聰明的數學家做出了巨大的努力,但這個問題仍然沒有得到解決。
這個問題被稱為 "科拉茨猜想"。
陷入混沌
但為什麽它這麽難解呢?畢竟,一個孩子都會明白這個遊戲的規則。它看起來非常簡單。
透過對小數位的科拉茨數列的初步觀察,我們沒有看到什麽出乎意料的情況,但當我們到了,例如,數位27,相應的序列是111步長,它在快速下降到1之前達到9232。
如果我們繪制27的科拉茨數列,我們會得到以下圖表。
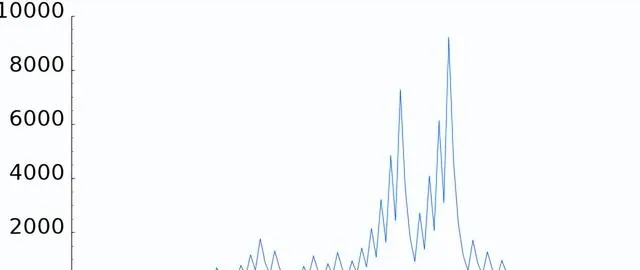
這看起來有點隨機,事實上,這個問題有一定的隨機性,這使得它很難處理。我們稍後會再討論這個問題。
請註意,如果n是一個奇數,那麽3n+1就是一個偶數,我們需要將其除以2,因此我們可以將這兩步合並為一步,簡單地說就是(3n+1)/2。
當我們把上述兩個步驟結合起來時,我們會把得到的數列稱為簡化的科拉茨數列。
考慮一下下面的函式。
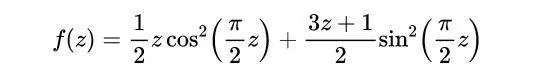
這個函式將輸出簡化後的科拉茨數列中的下一個數位,當然前提是z是一個整數。
但是這個函式,如果我們在複數平面上定義它,是一個完整的函式,這意味著我們可以給它輸入任何復數,而且它是復數可微的。
馬克-張伯倫研究了這個函式在實線上的叠代,結果發現,這導致了一個動態系統。他表明,這個猜想對於所有的正實數來說並不成立,因為存在著無限多的固定點以及軌域。
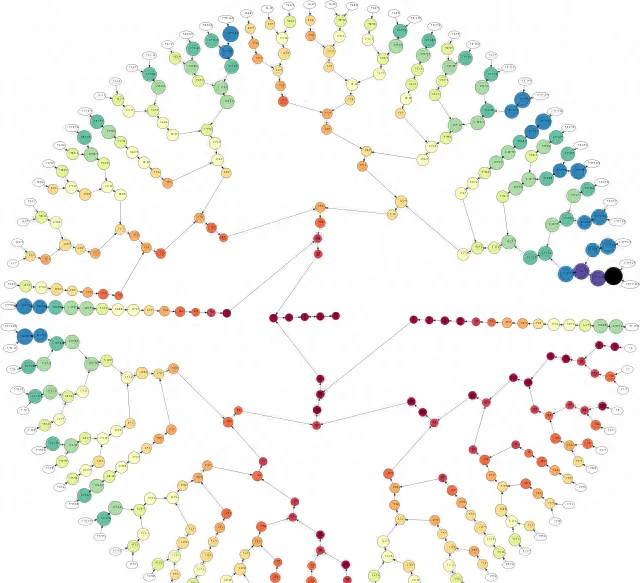
下面可以看到相應的美麗的科拉茨碎形。

這表明,這些數列確實有一些內在的混沌性。
眾所周知,動力系統和碎形源於混沌系統,例如天氣,其決定性特征是系統對初始條件極為敏感。
對於我們的問題來說,這意味著考慮整數和實數之間存在巨大差異,即使我們可以透過實數數列任意接近一個給定的整數,相應的科拉茨數列可能非常不同。這就造成了混亂。
解
那麽,解是什麽樣子的呢?我們需要證明兩件事。首先,我們需要證明所有數列都是有界的。換句話說,不存在無限的科拉茨數列。我所說的無限是指序列中的數位集是無限大的。第二,我們需要證明不可能出現迴圈。也就是說,在科拉茨數列中,我們永遠不會遇到一個數位兩次。如果我們從1開始,那麽4,2,1的序列就會無限期地重復。
當然,還有另一種解決辦法。這個猜想可能是錯的,數學家試圖驗證它,取的起始值約為2^68。1958年,波利亞猜想( Pòlya conjecture )被一個大約1.845×10^361的反例所推翻,這比2^68這數位大得多。
實際上,這裏還可能發生另一件事。數學家們往往不大談論這個問題,因為這是很悲傷的想法。科拉茨猜想在我們的公理系統中可能是無法解決的,也就是說,無論我們如何努力,我們都無法破解它。
不要被問題的美感所迷惑
那麽,為什麽說這是一個危險的問題呢?
因為,當你試圖解決一個數學問題,而你又不知道自己是否能夠解決它時,你就把寶貴的時間都花了,最終什麽也得不到。
時間是最寶貴的,而把它用在數學上是非常容易的,尤其是當一個問題看起來如此簡單的時候。但事實上它一點也不簡單。這就像希臘神話中的塞壬。
希臘神話中的塞壬一開始就是一群看起來像美女的生物,但實際上是吃人的野獸。他們坐在岸邊,用誘人的聲音唱歌,任何聽到他們歌聲的人都會被他們迷住。然後塞壬就會吃掉他們。
這個問題很像這樣。它看起來如此美麗和簡單,但在你意識到之前,你已經花費了多年的研究和精力,最終什麽都沒有。
實際上,許多教授警告他們的博士生不要去研究這個猜想。
真的會無功而返嗎
我只是部份同意上述觀點。就我個人而言,我花了很多很多時間思考黎曼假設、孿生質數猜想和科拉茨猜想,但我從不覺得自己浪費了時間,因為思考這些美麗的問題給我帶來快樂。
我喜歡這個過程和挑戰。即使你可能沒有更接近解決實際問題,但你可能在這個過程中發展出一些公理或一些其他工具。如果不出意外,你會體會到做原始研究的感覺,並加入到許多曾經走過這條路的人中。